PROBLEMS ON INTERSECTING LINES

Example 1 :

If x + 2y = 7 and 2x + y = 8 are the equations of the lines of two diameter of the circle, find the radius of the circle if the point (0, -2) lies on the circle.

Solution :

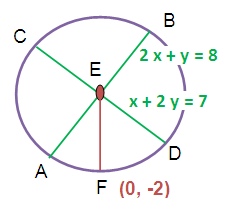
Two diameters are intersecting at the point E

x + 2y = 7 ----(1)

2x + y = 8 ----(2)

2(1) - (2) :

2(x + 2y) - (2x + y) =  14 - 8

2x + 4y - 2x - y = 6

3y = 6

y = 2

Substitute y = 2 in (1). 

x + 2(2) = 7

x + 4 = 7

x = 7 - 4

x = 3

Diameters are intersecting at the point E (3, 2).

So, center of the circle is E(3, 2). 

To find radius, find the distance between the points F and E. 

d = √[(x₂ - x₁)² + (y₂ - y₁)²]

Substitute (x₁, y₁) = E(3, 2) and (x₂, y₂) = F(0, -2). 

= √[(0 - 3)² + (-2 - 2)²]

= √(9 + 16)

= √25

= 5

Radius of the circle is 5 units.

Example 2 :

Find the equation of the straight line segment whose end points are the point of intersection of the straight lines

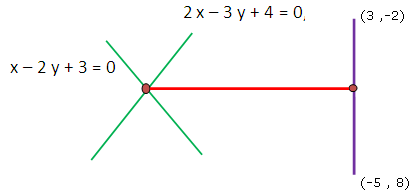
2x – 3y + 4 = 0, x – 2y + 3 = 0

and the midpoint of the line joining (3, -2) and (-5, 8).

Solution :

2x – 3y + 4 = 0 ----(1)

x – 2y + 3 = 0 ----(2)

Let A be the point of intersection of (1) and (2) and B be the midpoint of the line joining (3, -2) and (-5, 8).

Target : Find the equation of the line AB. 

(1) - 2(2) :

2x - 3y + 4 - 2(x - 2y + 3) = 0

2x - 3y + 4 - 2x + 4y - 6 = 0

y - 2 = 0

y = 2

Substitute y = 2 in (1). 

2x - 3(2) + 4 = 0

2x - 6 + 4 = 0

2x - 2 = 0

x = 1

Point of intersection of the lines (1) and (2) is A(1, 2).  

Find the midpoint of line joining (3, -2) and (-5, 8). 

Midpoint = ((x₁ + x₂)/2, (y₁ + y₂)/2)

= ((3 - 5)/2, (-2 + 8)/2)

= (-2/2, 6/2)

= B(-1, 3)

Find the slope of the line AB : 

m = (y₂ - y₁)/(x₂ - x₁)

Substitute (x₁, y₁) = A(1, 2) and (x₂, y₂) = B(-1, 3).

m = (3 - 2)/(-1 - 1)

= 1/(-2)

= -1/2

Equation of the line AB : 

y - y₁ = m(x - x₁)

Substitute (x₁, y₁) = A(1, 2) and m = -1/2.

y - 2 = (-1/2)(x - 1)

2(y - 2) = -1(x - 1)

2y - 4 = -x + 1

x + 2y - 5 = 0

Example 3 :

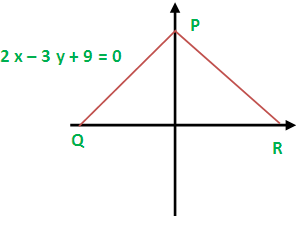
If the isosceles triangle PQR, PQ = PR. The base QR lies on the axis, P lies on the y-axis and

2x – 3y + 9 = 0

is the equation of PQ. Find the equation of PQ. Find the equation of the straight line along PR.

Solution :

To find the point point P which lies on the y-axis, substitute x = 0. 

2(0) - 3y = -9

-3y = -9

y = 3

The point P is (0, 3)

To find the point point Q which lies on the x-axis, substitute y = 0.

2x - 3(0) = -9

2x - 0 = -9

2x = -9

x = -9/2

The point Q is (-9/2 , 0)

The length of the sides PQ and PR are same. So the point R is (9/2,0)

Equation of PR :

(y-y₁)/(y₂-y₁) = (x-x₁)/(x₂-x₁)

Substitute (x₁, y₁) = P(3, 0) and (x₂, y₂) = R(9/2, 0).

(y - 3)/(0 - 3) = (x - 9/2)/(9/2 - 3)

(y - 3)/(-3) = (2x - 9)/(3/2)

-(y - 3) = 2(2x - 9)

- y + 3 = 4x - 18

4x + y - 21 = 0

Example 4 :

Find the equation of a straight line parallel to Y axis and passing through the point of intersection of the lines 4x + 5y = 13 and x - 8y + 9 = 0

Solution :

To find the point of intersection of these two lines

4x + 5y = 13 --------(1)

x - 8y + 9 = 0 --------(2)

(2) ⋅ (-4) ==> 4x + 5y = 13

                    -4x + 32y = 36

                    -----------------

                           37y = 49

y = 49/37

Applying the value of y in (1), we get

4x + 5(49/37) = 13

4x = 13 - (245/37)

4x = (481 - 245)/37

= 236/37

x = 236/37(4)

x = 59/37

Since the required line is parallel to y-axis, the slope will become 0.

y - y₁ = m(x - x₁)

y - 49/37 = (1/0)(x - 59/37)

0 = x - 59/37

37x - 59 = 0

Example 5 :

Find the equation of a straight line through the intersection of lines 7x + 3y = 10, 5x - 4y = 1 and parallel to the line 13x + 5y + 12 = 0

Solution :

7x + 3y = 10 ------(1)

5x - 4y = 1 -------(2)

(1) ⋅ 4 ==> 28x + 12y = 40

(2) ⋅ 3 ==> 15x - 12y = 3

               ----------------

43x = 43

x = 43/43

x = 1

Applying x = 1 in (1), we get

7(1) + 3y = 10

7 + 3y = 10

3y = 10 - 7

3y = 3

y = 1

So, the point of intersection is at (1, 1).

The required line is parallel to 13x + 5y + 12 = 0

5y = -13x - 12

y = (-13/5)x - (12/5)

Slope = -13/5

Equation of line :

(y - y₁) = m(x - x₁)

y - 1 =  -13/5 (x - 1)

5(y - 1) = -13(x - 1)

5y - 5 = -13x + 13

13x + 5y - 5 - 13 = 0

13x + 5y - 18 = 0

So, the required equation is 13x + 5y - 18 = 0.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.