FIND THE EQUATION OF THE MEDIAN AND ALTITUDE WITH VERTICES

Example 1 :

If the vertices of a triangle ABC are

A (2, -4), B (3, 3) and C (-1, 5).

Find the equation of the straight line along the altitude from vertex B.

Solution :

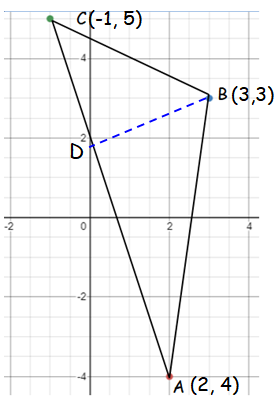
Slope of the line AC :

m  =  (y₂-y₁)/(x₂-x₁)

=  (5-(-4))/(-1-2)

=  (5+4)/(-3)

=  9/(-3)

m  =  -3  

Slope of BD  =  -1/(-3)

=  1/3

Equation of BD :

(y-y₁)  =  m(x-x₁)

(y-3)  =  (1/3)(x-3)

3(y-3)  =  1(x-3)

3y-9  =  x-3

x-3y-3+9  =  0

x-3y+6  =  0

Example 2 :

If the vertices of triangle ABC are (-4, 4) , B (8 ,4) and C (8, 10). Find the equation of the straight line along the median from A.

Solution :

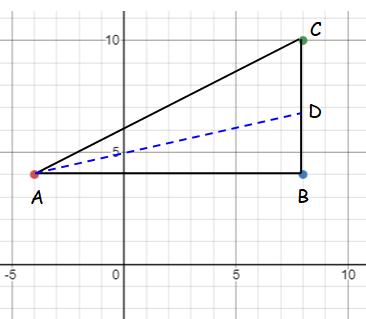
Slope of the line BC :

m  =  (y₂-y₁)/(x₂-x₁)

=  (10-4)/(8-8)

=  6/0

m  =  0

Slope of AD  =  -1/0

Equation of AD :

(y-y₁)  =  m(x-x₁)

(y-4)  =  (-1/0)(x-(-4))

0(y-4)  =  -1(x+4)

0  =  -x-4

x+4  =  0

Example 3 :

Find the coordinates of the foot from the origin on the straight line

3x+2y  =  13.

Solution :

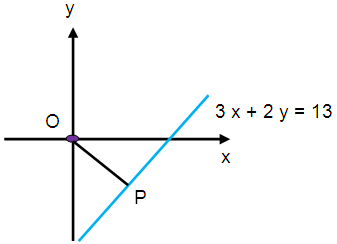
The line OP is perpendicular to the 3x+2y  =  13.

Equation of the line OP :

2x-3y+k  =  0

The line OP is passing through the origin (0 , 0)

2(0)-3(0)+k  =  0

k  =  0

So, equation of the line OP :

2x-3y+0  =  0

2x-3y  =  0

Both lines are intersecting at the point P.

3x+2y  =  13 -------- (1)

2x-3y  =  0 -------- (2)

3(1)+2(2) ==>

9x+6y+4x-6y  =  39+0

13x  =  39

x  =  3

By applying the value of x in (2), we get

2(3)-3y  =  0

6-3y  =  0

-3y  =  -6

y  =  2

So, the required point P is (3, 2).

Example 4 :

Find the equations of median drawn from the vertices A to BC and C to AB.

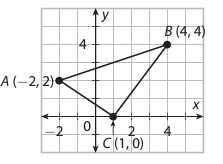
Solution :

Let AD be the median drawn from the point A to the side BC.

To find median of the drawn from the point A to BC, we have find the midpoint of the line segment BC

Midpoint = (x₁+x₂)/2, (y₁+y₂)/2

= (1+4)/2,(0+4)/2

= (5/2, 2)

Now we can find equation of the median AD drawn from the point A.

Slope of the median =  (y₂-y₁)/(x₂-x₁)

= (2 - 2) / (5/2 -2)

= 0/(1/2)

= 0

Equation of the median AD :

(y - y₁) = m(x - x₁)

A(-2, 2) and slope = 0

y - 2 = 0(x - (-2))

y - 2 = 0

y = 2

To find median of the drawn from the point C to AB, we have find the midpoint of the line segment AB

Midpoint = (x₁+x₂)/2, (y₁+y₂)/2

= (-2+4)/2, (2+4)/2

= (1, 3)

Now we can find equation of the median BC drawn from the point C.

Slope of the median =  (y₂-y₁)/(x₂-x₁)

(1, 0) and (1, 3)

= (3 - 0) / (1 - 1)

= 3/0

= undefined

Equation of the median BC :

(y - y₁) = m(x - x₁)

C(1, 0) and slope = 3/0

y - 0 = (3/0)(x - 1)

x - 1 = 0

x = 1

Example 5 :

A triangle has vertices J(4, -3), K(-1,- 2), and L(7, 3). Determine the equation of the altitude from vertex K.

Solution :

When we draw a perpendicular from the vertex K, it will intersect the opposite side JL with the angle measure of 90 degree.

Slope of JL = (y₂-y₁)/(x₂-x₁)

J(4, -3) and L(7, 3)

m = (3 - (-3)) / (7 - 4)

= (3+3)/3

= 6/3

= 2

Slope of altitude drawn from K :

= -1/2

Equation of altitude drawn from k :

(y - y₁) = m(x - x₁)

k(-1, -2) and slope = -1/2

y - (-2) = -1/2(x - (-1))

y + 2 = -1/2(x + 1)

2(y + 2) = -1(x + 1)

2y + 4 = -x - 1

x + 2y + 4 + 1 = 0

x + 2y + 5 = 0

Example 6 :

A triangle has vertices Q(6, -4), R(5, 2), and S(1, 4). Determine the equation of the perpendicular bisector of QR.

Solution :

Perpendicular bisector means, it must be perpendicular as well it will bisect the line segment into two parts.

Let T be the midpoint of QR.

Midpoint of QR :

= (6 + 5)/2, (-4 + 2)/2

= 11/2, -2/2

= T (11/2, -1)

Slope of QR  :

Q(6, -4), R(5, 2)

= (y₂ - y₁)/(x₂ - x₁)

= (2 + 4) / (5 - 6)

= 6 / -1

= -6

Slope of perpendicular line = 1/6

Equation of perpendicular bisector :

(y - y₁) = m(x - x₁)

(y - (-1)) = (1/6) (x - 11/2)

6(y + 1) = 1(2x - 11)/2

12(y + 1) = 2x - 11

12y + 12 = 2x - 11

2x - 12y - 11 - 12 = 0

2x - 12y - 23 = 0

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.