HOW TO FIND THE EQUATION OF A LINE WITH ONE POINT
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Question 1 :
Write the equations of
the straight lines parallel to x-axis which are at a distance of 5 units from
the x-axis
Solution :
The line which is drawn from above the x axis and parallel to the x axis will be a horizontal line.
So, the required equations will be y = 5 and y = -5.
Question 2 :
Find the equations of the straight lines parallel to the coordinates axes and passing through the point (-5, -2)
Solution :
via one point, we can draw infinite number of lines. Since the required lines will be parallel to x and y axis, we can draw two lines as follows.
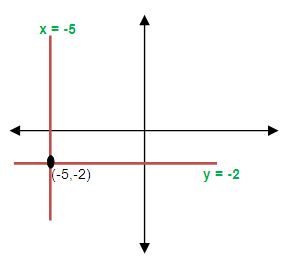
Therefore the two required equations are
y = -2 and x = -5.
Question 3 :
Find the equation of a straight line whose
(i) Slope is -3 and y-intercept is 4.
Solution :
Slope (m) = -3
Y-intercept (b) = 4
Equation of the straight line:
y = mx + b
y = 3x + 4
So, the required equation of the line y = 3x+4.
(ii) Angle of inclination is 60 degree and y-intercept is 3.
Solution :
Slope (m) = tan θ
m = tan 60
m = √3
y-intercept (b) = 3
Equation of the straight line :
y = mx + b
y = √3x + 3
So, the required equation of the line y = √3x + 3.
Question 4 :
Find the equation of the line intersecting the y-axis at a distance of 3 units above the origin and
tan θ = 1/2
where Ѳ is the angle of inclination.
Solution :
The required line is intersecting the y-axis at a distance of 3 units above the origin. So we can take y-intercept as 3
tan θ = 1/2
m = 1/2
Equation of the straight line :
y = mx + b
y = (1/2)x + 3
y = (x + 6)/2
2y = x + 6
x – 2y + 6 = 0
Question 5 :
Find the equation of the straight line which passes through the midpoint of the line segment joining
(4, 2) and (3, 1)
whose angle of inclination is 30 degree.
Solution :
First we have to find midpoint of the line segment joining the points (4, 2) and (3, 1)
Midpoint = (x1 + x2)/2, (y1 + y2)/2
= (4 + 3)/2, (2 + 1)/2
= (7/2, 3/2)
angle of inclination = 30°
θ = 30°
Slope (m) = tan θ
m = tan 30°
m = 1/√3
Equation of the line :
(y - y1) = m(x - x1)
(y - (3/2)) = (1/√3)(x - (7/2))
(2y - 3) = (1/√3)(2x - 7)
2√3y - 3√3 = 2x - 7
2x - 2√3y - 7 + 3√3 = 0
Question 6 :
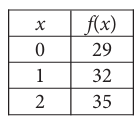
For the linear function f, the table shows three values of x and their corresponding values of f x equation defines f(x) ?
a) f(x) = 3x + 29 b) f(x) = 29x + 32
c) f(x) = 35x + 29 d) f(x) = 32x + 35
Solution :
From the table, choosing two points from the table (0, 29) and (1, 32) we find the slope.
Slope = (32 - 29) / (1 - 0)
= 3/1
= 3
y-intercept is 29
Equation of the line :
y = mx + b
y = 3x + 29
So, option a is correct.
Question 7 :
Hana deposited a fixed amount into her bank account each month. The function
f(t) = 100t + 25
gives the amount, in dollars, in Hana’s bank account after t monthly deposits. What is the best interpretation of 25 in this context?
a) With each monthly deposit, the amount in Hana’s bank account increased by $25.
b) Before Hana made any monthly deposits, the amount in her bank account was $25.
c) After 1 monthly deposit, the amount in Hana’s bank account was $25.
d) Hana made a total of 25 monthly deposits.
Solution :
f(t) = 100t + 25
Here t represents monthly deposits and f(t) will be the amount.
f(1) = 100 + 25 ==> 125
f(2) = 200 + 25 ==> 225
So, option b, before Hana made any monthly deposits, the amount in her bank account was $25 is correct.
Question 8 :
Which of the following equations represents a line that passes through (7, 6) and is parallel to the -x axis?
A) x = 6 B) x = 7 C) y = 6 D) y = 7
Solution :
Via a point we can draw infinite number of lines, since we are drawing a line which is parallel to x-axis the required equation will be x = 7.
Question 9 :
Which of the following equations represents a line that passes through (-5, 1) and is parallel to the y axis?
A) y = -5 B) y = 1 C) x = -5 D) x = 1
Solution :
Equation of a line which is parallel to y-axis will be in the form y = a. So, the required equation will be
y = 1
Question 10 :
f(x) = ax + 2
In the function above, a is a constant. If f(-1) = 4, what is the value of f(-1/2) ?
Solution :
f(x) = ax + 2
f(-1) = 4
Applying x = -1 and y = 4
4 = a(-1) + 2
4 - 2 = -a
-a = 2
a = -2, then
f(x) = -2x + 2
Now applying -1/2 for x, we get
f(-1/2) = -2(-1/2) + 2
= 1 + 2
= 3
So, the value of f(-1/2) is 3.
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
About Us | Contact Us | Privacy Policy
©All rights reserved. onlinemath4all.com
Recent Articles
-
Quantitative Reasoning Questions and Answers
Dec 14, 25 06:42 AM
Quantitative Reasoning Questions and Answers -
Specifying Units of Measure
Dec 14, 25 06:38 AM
Specifying Units of Measure -
Coin Tossing Probability
Dec 13, 25 10:11 AM
Coin Tossing Probability - Concept - Sample Space - Formula - Solved Problems