EQUATION OF A STRAIGHT LINE WORKSHEET

Problem 1 :

Find the equations of the straight lines parallel to the coordinate axes and passing through the point (3, -4).

Problem 2 :

Find the general equation of the straight line whose angle of inclination is 45° and y-intercept is 2/5.

Problem 3 :

Find the general equation of the straight line passing through the point (-2, 3) with slope 1/3.

Problem 4 :

Find the general equation of the straight line passing through the points (-1, 1) and (2, -4). 

Problem 5 :

The vertices of a triangle ABC are A(2, 1), B(-2, 3) and C(4, 5). Find the equation of the median through the vertex A.

Problem 6 :

If the x-intercept and y-intercept of a straight line are 2/3 and 3/4 respectively, find the general equation of the straight line. 

Problem 7 :

Find the equations of the straight lines each passing through the point (6, -2) and whose sum of the intercepts is 5.

Problem 8 :

Find the general equations of the straight lines parallel to x- axis which are at a distance of 5 units from the x-axis.

Problem 9 :

Find the slope and y-intercept of the straight line whose equation is 4x - 2y + 1  =  0. 

Problem 10 :

A straight line has the slope 5. If the line cuts y-axis at -2, find the general equation of the straight line. 

Answers

1. Answer :

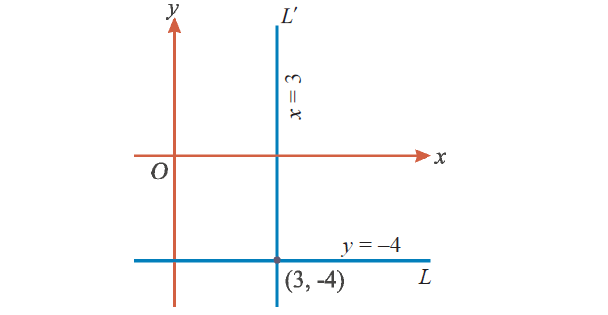
Let L and L' be the straight lines passing through the point (3, -4) and parallel to x-axis and y-axis respectively.

The y-coordinate of every point on the line L is – 4.

Hence, the equation of the line L is

y  =  - 4

Similarly, the x-coordinate of every point on the straight line L' is 3

So, the equation of the line L' is

x  =  3

2. Answer :

From the angle of inclination 45°, we can get the slope.

Slope of the line m  =  tan45°  =  1

Given : y-intercept b  =  2/5 

So, the equation of the straight line in slope-intercept form is

y  =  mx + b 

Substitute m  =  1 and b  =  2/5.

y  =  1x + 2/5

Multiply each side by 5. 

5y  =  5x + 2

Subtract 5y from each side.

0  =  5x - 5y + 2

or

5x - 5y + 2  =  0

So, the general equation of straight line is

5x - 5y + 2  =  0

3. Answer :

Given : Point  =  (-2, 3)  and  slope  m  =  1/3

So, the equation of the straight line in point-slope form is 

y - y₁  =  m(x - x₁)  

Substitute (x₁ , y₁) = (-2 , 3) and m = 1/3. 

y - 3  =  1/3 ⋅ (x + 2)

Multiply each side by 3.

3(y - 3)  =  x + 2

Simplify. 

3y - 9  =  x + 2

Subtract 3y from each side. 

-9  =  x - 3y + 2

Add 9 to each side.

0  =  x - 3y + 11

So, the general equation of straight line is

x - 3y + 11 = 0

4. Answer :

Given : Two points on the straight line : (-1, 1) and  (2, -4).

So, the equation of the straight line in two-points form is 

(y - y₁)/(y₂ - y₁)  =  (x - x₁)/(x₂ - x₁)

Substitute (x₁ , y₁)  =  (-1, 1) and (x₂, y₂)  =  (2, -4).

(y - 1)/(-4 - 1)  =  (x + 1)/(2 + 1)

Simplify.

(y - 1)/(-5)  =  (x + 1)/3

Cross multiply.

3(y - 1)  =  -5(x + 1)

3y - 3  =  -5x - 5

5x + 3y + 2  =  0  

So, the general equation of straight line is

5x + 3y + 2  =  0

5. Answer :

Median is a straight line joining a vertex and the midpoint of the opposite side.

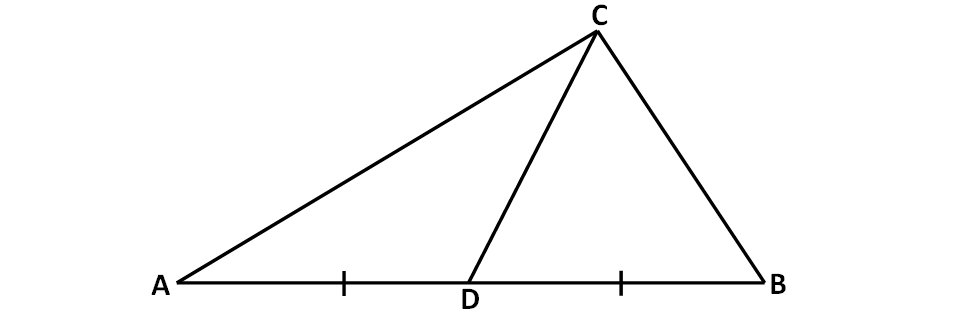
Let D be the midpoint of BC.

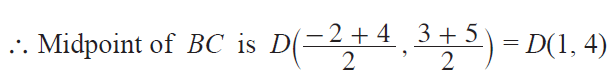
The median through A is nothing but the line joining two points A (2, 1) and D(1, 4). 

So, the equation of the median through A is 

(y - y₁)/(y₂ - y₁)  =  (x - x₁)/(x₂ - x₁)

Substitute (x₁ , y₁) = (2, 1) and (x₂, y₂)  =  (1, 4). 

(y - 1)/(4 - 1)  =  (x - 2)/(1 - 2)

Simplify. 

(y - 1)/3  =  (x - 2)/(-1)

Cross multiply.

-1(y - 1)  =  3(x - 1)

Simplify.

-y + 1 = 3x - 3

3x + y - 4 = 0     

So, the equation of the median through A is 

3x + y - 4  =  0

6. Answer :

Given :

x- intercept  "a"  =  2/3

y-intercept  "b"  =  3/4

So, the equation of the straight line in intercept form is 

x/a  +  y/b  =  1

Substitute a  =  2/3  and  b  =  3/4. 

x/(2/3)  +  y/(3/4)  =  1

Simplify.

3x/2  +  4y/3  =  1

(9x + 8y)/6  =  1

Multiply each side by 6. 

9x + 8y  =  6

Subtract 6 from each side from 6. 

9x + 8y - 6  =  0  

So, the general equation of straight line is

9x + 8y - 6  =  0

7. Answer :

Let "a" and "b" be the x-intercept and y-intercept of the required straight line respectively. 

Given : Sum of the intercepts  =  5

So, we have  

a + b  =  5

Subtract a from each side.

b  =  5 - a

Now, equation of the straight line in intercept form is 

x/a  +  y/b  =  1

Plugging  b  =  5 - a, we get 

x/a  +  y/(5 -  a)  =  1

Simplify.

[(5 - a)x + ay]/a(5 - a)  =  1

(5 - a)x + ay  =  a(5 - a) -----(1)

The straight line is passing through (6, -2).

So, substitute (x, y)  =  (6, -2). 

(5 - a)6 - 2a  =  a(5 - a)

30 - 6a - 2a  =  5a - a²

a² - 13a + 30  =  0 

a² - 13a + 30  =  0

(a - 10)(a - 3) = 0 

a  =  10 and a  =  3 

When a = 10,

 (1)-----> (5 - 10)x + 10y  =  10(5 - 10)

- 5x + 10y  =  - 50

5x - 10y  - 50  =  0 

x - 2y - 10  =  0

When a = 3,

(1)----->(5 - 3)x + 3y  =  3(5 - 3)

2x + 3y  =  6

So, x - 2y - 10 = 0 and 2x + 3y - 6 = 0 are the general equations of the required straight lines.

8. Answer :

From the given information, we can sketch the two lines as given below. 

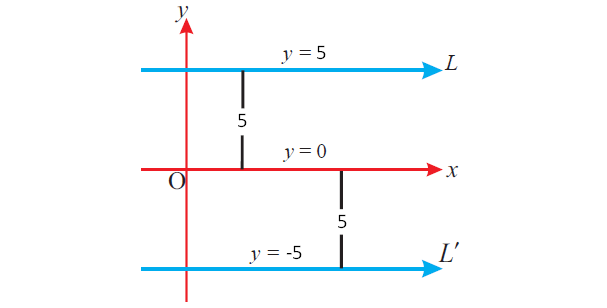
One line is above the x-axis at a distance of 5 units. And another line is below the x-axis at a distance of 5 units. 

So, y = 5 and y = -5 are the required straight lines. 

9. Answer :

Since we want to find the slope and y-intercept, let us write the given equation 4x - 2y + 1  = 0 in slope-intercept form. 

4x - 2y + 1  = 0

4x + 1  =  2y

Divide each side by 2. 

(4x + 1)/2  =  y

2x + 1/2  =  y 

or

y  =  2x + 1/2

The above form is slope intercept form. 

If we compare y  =  2x + 1/2  and  y  =  mx + b, we get  

m  =  2     and     b  =  1/2

So, the slope is 2 and y-intercept is 1/2.

10. Answer :

Since the line cuts y-axis at -2, clearly y-intercept is -2.

So, the slope m  =  5 and y-intercept b  =  -2.

Equation of a straight line in slope-intercept form :

y  =  mx + b

Substitute m  =  5  and  b  =  -2

y  =  5x - 2

Subtract y from each side. 

5x - y - 2  =  0

So, the general equation of the required line is

5x - y - 2  =  0

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.