EASY WAY TO FIND FACTORS OF A LARGE NUMBER

Factors are numbers we can multiply together to get a number.

To find the number of factors of an integer, we need to follow the steps given below.

Step 1 : 

Split the given number as prime factors using prime factorization method or tree method.

Step 2 : 

Take all exponents and add one to each of them.

Step 3 : 

Multiply the modified exponents together.

Example 1 :

Find the number of factors of 48.

Solution :

Method 1 :

Decompose 48 into prime factors as shown below. 

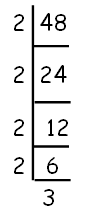
48  =  2⁴ x 3¹

Modified exponents are (4 + 1) and (1 + 1). 

That is, 5 and 2. 

Multiplying the modified exponents.

5 x 2  =  10

Number of factors of 48 is 10.

Method 2 :

To get the number of factors of 48, first we have to find the factors.

48  =  1 x 48

48  =  2 x 24

48  =  3 x 16

48  =  4 x 12

48  =  6 x 8

Factors of 48 are 1, 2, 3, 4, 6, 8, 12, 16, 24 and 48.

Number of factors of 48 = 10. 

Example 2 :

Find the number of factors of 30.

Solution :

Decompose 30 into prime factors as shown below. 

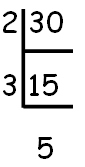
30  =  2¹ x 3¹ x 5¹

Modified exponents are (1 + 1), (1 + 1) and (1 + 1). 

That is, 2, 2 and 2. 

Multiplying the modified exponents.

2 x 2 x 2  =  8

Number of factors of 30 is 8.

Example 3 :

Find the number of factors of 42. 

Solution :

Decompose 42 into prime factors as shown below. 

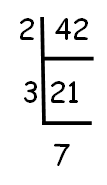
42  =  2¹ x 3¹ x 7¹

Modified exponents are (1 + 1), (1 + 1) and (1 + 1). 

That is, 2, 2 and 2. 

Multiplying the modified exponents.

2 x 2 x 2  =  8

Number of factors of 42 is 8.

Apart from the stuff given above, if you need any other stuff in math, please use our google custom search here.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.