DRAWING PIE CHART
About "Drawing pie chart"
Drawing pie chart :
Here, we take a circle and the whole circle is divided into sectors. The size of each sector is proportional to the activity or information it represents.
Since, the sectors resemble the slices of a pie, it is called a pie chart.
Construction of pie chart - Important note
In a pie chart, the various observations or components are represented by the sectors of a circle and the whole circle represents the sum of the value of all the components .Clearly, the total angle of 360° at the center of the circle is divided according to the values of the components .
The central angle of a component is
= [ Value of the component / Total value] x 360°
Sometimes, the value of the components are expressed in percentages. In such cases,
The central angle of a component is
= [ Percentage value of the component / 100 ] x 360°
Steps for construction of pie chart
Step 1 :
Calculate the central angle for each component , using the above formula.
Step 2 :
Draw a circle of convenient radius.
Step 3 :
Within this circle, draw a horizontal radius.
Step 4 :
Draw radius making central angle of first component with horizontal radius; this sector represents the first component. From this radius, draw next radius with central angle of second component; this sector represents second component and so on, until we exhaust all components.
Step 5 :
Shade each sector differently and mark the component it represents.
Step 6 :
Give the heading for each component.
Construction of pie chart - Examples
Example 1 :
The following table shows the half yearly budget of a family
|
Particulars Food House rent Clothing Education Savings Miscellaneous |
Expenses (in $) 4800 2400 1600 800 1000 1400 |
Draw a pie chart to represent the above information.
Solution :
The central angle of a component is
= [ Value of the component / Total value] x 360°
We may calculate the central angles for various components as follows :
|
Particulars Food House rent Clothing Education Savings Miscellaneous ------------ Total |
Expenses 4800 2400 1600 800 1000 1400 ---------- 12000 |
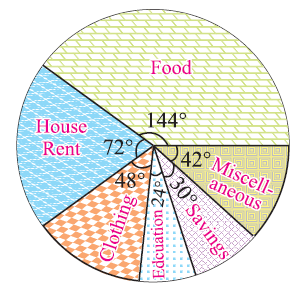
Central angle (4800/12000) ⋅ 360 = 144° (2400/12000) ⋅ 360 = 72° (1600/12000) ⋅ 360 = 48° (800/12000) ⋅ 360 = 24° (1000/12000) ⋅ 360 = 30° (1400/12000) ⋅ 360 = 42° |
From the above table, clearly, we obtain the required pie chart as shown below.
Example 2 :
The number of hours spent by a school student on various activities on a working day, is given below. Construct a pie chart using the angle measurement.
|
Activity Sleep School Play Homework Others |
Number of hours 8 6 3 3 4 |
Draw a pie chart to represent the above information.
Solution :
The central angle of a component is
= [ Value of the component / Total value] x 360°
We may calculate the central angles for various components as follows :
|
Activity Sleep School Play Homework Others ----------- Total |
Duration in hours 8 6 3 3 4 ---------- 24 |
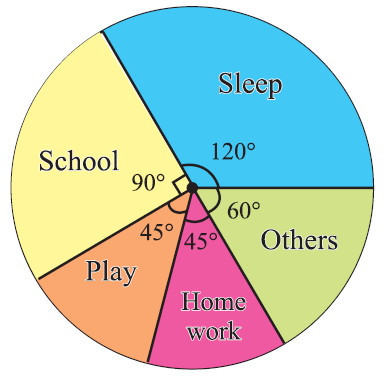
Central angle (8/24) ⋅ 360 = 120° (6/24) ⋅ 360 = 90° (3/24) ⋅ 360 = 45° (3/24) ⋅ 360 = 45° (4/24) ⋅ 360 = 60° 360° |
From the above table, clearly, we obtain the required pie chart as shown below.
Example 3 :
The result of an examination of a school is as follows :
|
Result Passed in first class Passed in second class Passed in third class Failed |
Percentage of students 25% 35% 30% 10% |
Draw a pie chart to represent the above information.
Solution :
The central angle of a component is
= [ Value of the component / 100 ] x 360°
We may calculate the central angles for various components as follows :
|
Result Passed in first class Passed in second class Passed in third class Failed ---------- Total |
Percentage of students 25% 35% 30% 10% ----------- 100% |
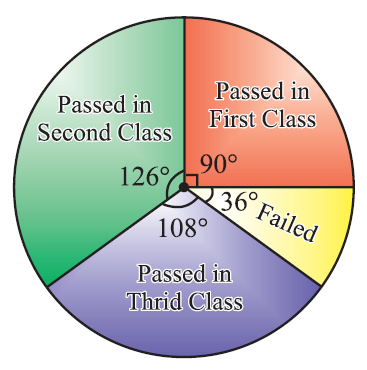
Central angle (25/100) ⋅ 360 = 90° (35/100) ⋅ 360 = 126° (30/100) ⋅ 360 = 108° (10/100) ⋅ 360 = 36° ------------- 360° |
From the above table, clearly, we obtain the required pie chart as shown below.
After having gone through the stuff given above, we hope that the students would have understood "Drawing pie chart".
Apart from the stuff given above, if you want to know more about "Drawing pie chart".
Apart from the stuff given on this web page, if you need any other stuff in math, please use our google custom search here.
You can also visit our following web pages on different stuff in math.
WORD PROBLEMS
Word problems on simple equations
Word problems on linear equations
Word problems on quadratic equations
Area and perimeter word problems
Word problems on direct variation and inverse variation
Word problems on comparing rates
Converting customary units word problems
Converting metric units word problems
Word problems on simple interest
Word problems on compound interest
Word problems on types of angles
Complementary and supplementary angles word problems
Markup and markdown word problems
Word problems on mixed fractrions
One step equation word problems
Linear inequalities word problems
Ratio and proportion word problems
Word problems on sets and venn diagrams
Pythagorean theorem word problems
Percent of a number word problems
Word problems on constant speed
Word problems on average speed
Word problems on sum of the angles of a triangle is 180 degree
OTHER TOPICS
Time, speed and distance shortcuts
Ratio and proportion shortcuts
Domain and range of rational functions
Domain and range of rational functions with holes
Graphing rational functions with holes
Converting repeating decimals in to fractions
Decimal representation of rational numbers
Finding square root using long division
L.C.M method to solve time and work problems
Translating the word problems in to algebraic expressions
Remainder when 2 power 256 is divided by 17
Remainder when 17 power 23 is divided by 16
Sum of all three digit numbers divisible by 6
Sum of all three digit numbers divisible by 7
Sum of all three digit numbers divisible by 8
Sum of all three digit numbers formed using 1, 3, 4
Sum of all three four digit numbers formed with non zero digits
Recent Articles
-
Algebra Worksheets in Math
Sep 23, 19 07:57 AM
Algebra Worksheets in Math - Concepts and practice questions with step by step solution
-
Solving Word Problems with Nature of Roots of Quadratic Equation
Sep 23, 19 05:08 AM
Solving Word Problems with Nature of Roots of Quadratic Equation - Concept and examples with step by step solution
-
Nature of Roots of Quadratic Equation Discriminant Examples
Sep 23, 19 04:47 AM
Nature of Roots of Quadratic Equation Discriminant Examples - Concept and examples with step by step solution
