DRAWING A HISTOGRAM WHEN CLASS INTERVALS ARE NOT CONTINUOUS

A two dimensional graphical representation of a continuous frequency distribution is called a histogram.

In histogram, the bars are placed continuously side by side with no gap between adjacent bars. That is, in histogram rectangles are erected on the class intervals of the distribution. The areas of rectangle are proportional to the frequencies.

Now let us look at the steps followed in drawing histogram for grouped data.

Step 1 :

Represent the data in the continuous (exclusive) form if it is in the discontinuous (inclusive) form.

Step 2 :

Mark the class intervals along the X-axis on a uniform scale.

Step 3 :

Mark the frequencies along the Y-axis on a uniform scale.

Step 4 :

Construct rectangles with class intervals as bases and corresponding frequencies as heights.

The method of drawing a histogram is explained in the following example.

Solved Examples

Example 1 :

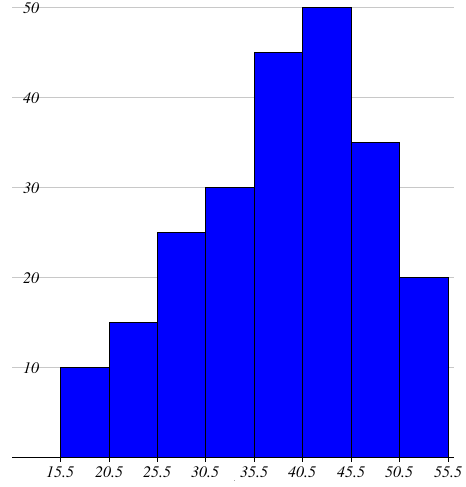
The heights of trees in a forest are given as follows. Draw a histogram to represent the data.

Solution :

In this problem, the given class intervals are discontinuous (inclusive) form.

If we draw a histogram as it is, we will get gaps between the class intervals. But in

a histogram the bars should be continuously placed without any gap. Hence we should make the class intervals continuous. For this we need an adjustment factor. 

Adjustment Factor

  =  (1/2) [(lower limit of a class interval) – (upper limit of the preceding class interval)]

= (1/2)(21 – 20) = 0.5

In the above class interval, we subtract 0.5 from each lower limit and add 0.5 in each upper limit. Therefore we rewrite the given table into the following table.

Scale :

X - axis  =  1 cm  =  5 meters

Y - axis  =  1 cm  =  5 trees

Example 2 :

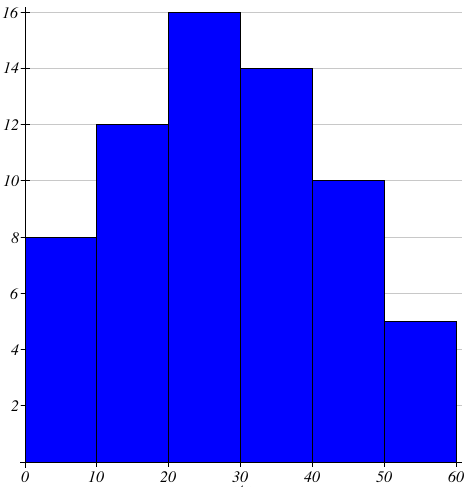
Draw a histogram to represent the following data

Scale :

X - axis  =  1 cm  =  10 units

Y - axis  =  1 cm  =  2 units

Example 3 :

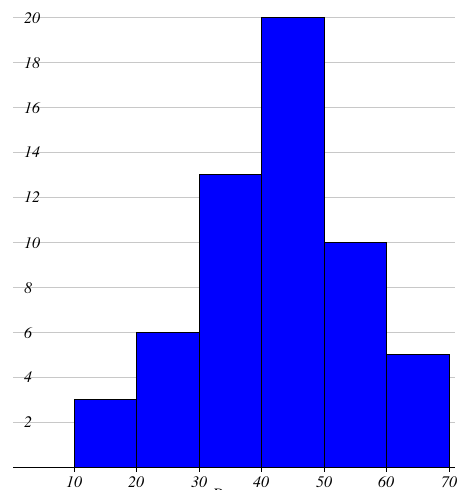
In a study of diabetic patients in a village, the following observations were noted. Represent the above data by a frequency polygon using histogram.

Scale :

X - axis  =  1 cm  =  10 age

Y - axis  =  1 cm  =  2 patients

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.