DOMAIN AND RANGE OF RATIONAL FUNCTIONS

Domain of a Rational Function

Let y  =  f(x) be a function.

Domain is all real values of x for which y is defined.

If there is any value of x for which y is undefined, we have to exclude that particular value from the set of domain. 

Example 1 :

Let us consider the rational function given below.

y  =  1/(x - 2)

In the above rational function, let us equate the denominator 'x  - 2' to zero.

x - 2  =  0

x  =  2

In the function

y  =  1/(x - 2),

if x = 2, then the denominator becomes zero and the value of 'y' becomes undefined.  

So, 'y' is defined for all real values of 'x' except x = 2.

Therefore, the domain is

R - {2}

Range of a Rational Function

Let y = f(x) be a function.

Range is nothing but all real values of y for the given domain (real values of x). 

Example 2 :

Let us consider the rational function given below.

y  =  1/(x - 2)

To find range of the rational function above, first we have to find inverse of y.

To find inverse of y, follow the steps given below.

Step 1 :

y = 1/(x - 2) has been defined by y in terms x. 

The same function has to be redefined by x in terms of y.

Step 2:

y = 1/(x - 2)

Multiply each side by (x - 2). 

(x - 2)y  =  1

xy - 2y  =  1

Add 2y to each side. 

xy  =  2y + 1

Divide each side by y.

x  =  (2y + 1) / y

Now the function has been defined by x in terms of y.

Step 3:

In x = (2y + 1) / y, we have to replace x by y^-1 and y by x.

Then, 

y^-1  =  (2x + 1) / x

Step 4:

Now, find the domain of y^-1.

In the inverse function y^-1, if we substitute 0 for x, the denominator becomes zero and the value of y^-1 becomes undefined.

y^-1 is defined for all real values of x except zero.

So, the domain of y^-1 is 

R - {0}

And we already know the fact that

Range (y)  =  Domain (y^-1)

Therefore, the range of y is

R - {0}

Another Way to Find Range of Rational Functions

For some rational functions, it is bit difficult to find inverse function. In that case, we have to sketch the graph of the rational function using vertical asymptote, horizontal asymptote and table of values as given below.

In this way, we can easily get the range of rational functions.

Let us see, how to find range of the rational function given below. 

y  =  1/(x - 2)

Vertical Asymptote :

To find vertical asymptote, we have to make the denominator (x - 2) equals to zero.

When we do so,   

x - 2  =  0

x  =  2

So, the vertical asymptote is  

x  =  2

Horizontal Asymptote :

In the rational function y  =  1 / (x - 2), the highest exponent of the numerator is less than the highest exponent of the denominator. 

So there is an horizontal asymptote. 

The equation of the horizontal asymptote is

y  =  0

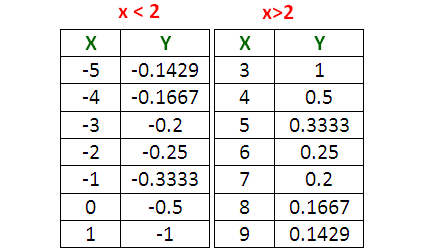
Table of Values :

In the given rational function y  =  1/(x-2), now we have to substitute some random values for x and find the corresponding values of y. 

We have already known that the vertical asymptote is

x  =  2 

Now, we have to take some random values for x in the following intervals.

x < 2, x > 2 but not x  =  2

(Because, x  =  2 is vertical asymptote)

Graph of 'y = 1/(x - 2)'

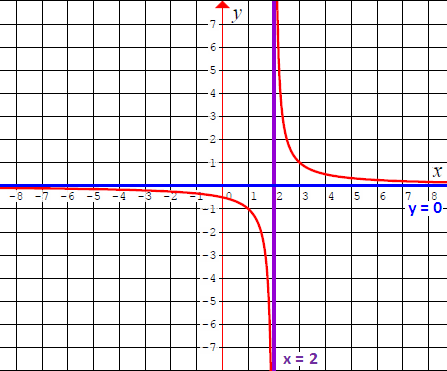
When we look at the above graph, the following point is very clear.

That is, the graph (in red color) of the rational function

y = 1/(x - 2)

appears at every real value of y except y  =  0.

From the graph, clearly, the range of y is 

R - {0}

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.