DOMAIN AND RANGE OF INVERSE TRIGONOMETRIC FUNCTIONS

In this section, you will learn how to find domain and range of inverse trigonometric functions. 

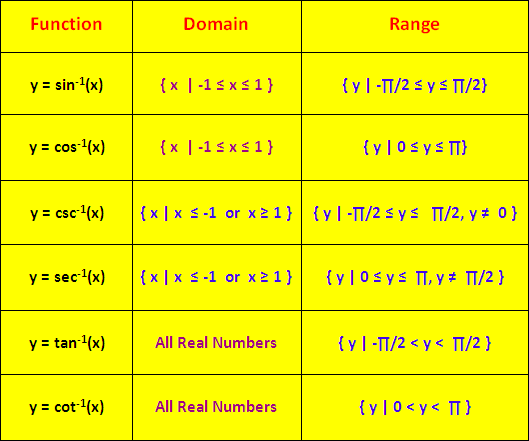
To make you to understand the domain and range of an inverse trigonometric function, we have given a table which clearly says the domain and range of inverse trigonometric functions.

Rule to Find Domain of Inverse Trigonometric Functions

For any trigonometric function, we can easily find the domain using the below rule.

That is, 

                       Domain (y^-1)  =  Range (y)

More clearly, from the range of trigonometric functions, we can get the domain of inverse trigonometric functions. It has been explained clearly below.

Domain of  Inverse Trigonometric Functions

Already we know the range of sin(x).

That is, range of sin(x) is

[-1, 1]

And also, we know the fact,

Domain of inverse function = Range of the function. 

So, domain of sin^-1(x) is 

[-1, 1]  or  -1 ≤ x ≤ 1

In the above table, the range of all trigonometric functions are given.

From the fact, 

"Domain of inverse function = Range of the function",

we can get the domain of all inverse trigonometric functions.  

Domain of sin^-1(x)  =  [-1, 1]  

Domain of cos^-1(x)  =  [-1, 1]  

Domain of csc^-1(x)  =  (-∞, -1]   or  [1, +∞)

Domain of sec^-1(x)  =  (-∞, -1]   or  [1, +∞)

Domain of tan^-1(x)  =  All Real Numbers

Domain of cot^-1(x)  =  All Real Numbers

Rule to Find Range of Inverse Trigonometric Functions

Even though there are many ways to restrict the range of inverse trigonometric functions, there is an agreed upon interval used.

That is ,

[-π/2 ,  π]

We have to split the above interval as parts and each part will be considered as range which depends upon the given inverse trigonometric function.

The length of each part must be π or 180° .

When we try to get range of inverse trigonometric functions, either we can start from -π/2 or 0 (Not both).

If we start from -π/2, the range has to be restricted in the interval

[-π/2, π/2], Length  =  180° 

If we start from 0, the range has to be restricted in the interval    

[0, π], Length  =  180°

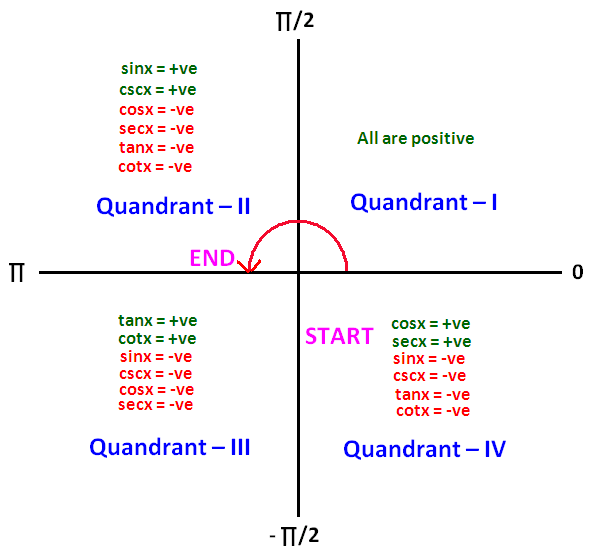
In the common range interval [-π/2, π], three quadrants are covered.

They are, quadrant IV, quadrant I and quadrant II.

For any inverse trigonometric function, we have to choose only two quadrants in the interval [-π/2, π]. In one the two quadrants, the trigonometric function should be positive and in the other quadrant, it should be negative.

For all inverse trigonometric functions, we have to consider only the first quadrant for positive. (Not any other quadrant)

Based on this, we have to decide the starting point.

That is either -π/2 or 0.

Range of sin⁻¹(x)

As explained above, sin x is positive in  the first quadrant (only first quadrant to be considered) and negative in the fourth quadrant of the common interval [-π/2, π].

These two quadrant are covered by the interval

[-π/2, π/2]

So, the range of y  =  sin^-1(x) is

[-π/2, π/2]

More clearly, the range of y  =  sin^-1(x) is ,

-π/2 ≤ y ≤ π/2

Range of cos⁻¹(x)

As explained above, cos x is positive in  the first quadrant (only first quadrant to be considered) and negative in the second quadrant of the common interval [-π/2, π] .

These two quadrant are covered in by the interval [0, π]

So, the range of y  =  cos^-1(x) is

[0, π]

More clearly, the range of y =  cos^-1(x) is

0 ≤ y ≤ π

Range of csc⁻¹(x)

As explained above, csc x is positive in  the first quadrant (only first quadrant to be considered) and negative in the fourth quadrant of the common interval [-π/2, π].

These two quadrant are covered by the interval

[-π/2, π/2]

We may consider [-π/2, π/2] as range of y = csc^-1(x). But, there is a value 0 in the interval [-π/2, π/2] for which we have

csc (0)  =  1 / sin(0)  =  1/0  =  Undefined.

So "0" can not be considered as a part of the range of

y = csc^-1(x)

So, the range of y  =  csc⁻¹(x) is

[-π/2, π/2] - {0}

More clearly, the range of y  =  csc^-1(x) is ,

-π/2 ≤ y ≤ π/2,  y ≠ 0

Range of sec⁻¹(x)

As explained above, sec x is positive in  the first quadrant (only first quadrant to be considered) and negative in the second  quadrant of the common interval [-π/2, π].

These two quadrant are covered by the interval [0, π]

We may consider [0, π] as range of y  =  sec^-1(x).

But, there is a value π/2 in the interval [0, π] for which we have

sec (π/2)  =  1 / cos (π/2)  =  1/0  =  Undefined.

So "π/2" can not be considered as a part of the range of

y = sec^-1(x)

So, the range of y  =  sec^-1(x) is

[0, π] - {π/2}

More clearly, the range of y  =  sec^-1(x) is

0 ≤ y ≤ π,   y ≠ π/2

Range of tan⁻¹(x)

As explained above, tan x is positive in  the first quadrant  (only first quadrant to be considered) and negative in both the second and fourth quadrants of the common interval [-π/2, π].

Case 1 :

If we consider the first quadrant for positive and second quadrant for negative, we get the interval [0, π] as range of y  =  tan^-1(x).

Note : Starting point is 0.

Case 2 :

If we consider the first quadrant for positive and fourth quadrant for negative, we get the interval [-π/2, π/2] as range of y  =  tan^-1(x).

Note : Starting point is -π/2.

When we consider the first case, we will get the interval [0, π] as range of  y = tan^-1(x). But there is a value π/2 in the middle  of the interval [0, π] for which we have

tan (π/2)  =  undefined

So we can not consider π/2 as a part of the range of

y  =  tan^-1(x)

So we can ignore case 1 and consider case 2. 

When we consider case 2, we get the interval

[-π/2, π/2]

as range of y = tan^-1(x).

Even though we get the interval [-π/2, π/2] as range of

y  =  tan^-1(x),

tan x becomes undefined for the two corner values -π/2 and π/2.

So -π/2 and π/2 can not be considered as parts of the range of

y  =  tan^-1(x).

So, the range of y  =  tan^-1(x) is

(-π/2, π/2)

More clearly, the range of y  =  tan^-1(x) is ,

-π/2 < y < π/2

Range of cot⁻¹(x)

As explained above, cot x is positive in  the first quadrant  (only first quadrant to be considered) and negative in both the second and fourth quadrants of the common interval [-π/2, π].

Case 1 :

If we consider the first quadrant for positive and second quadrant for negative, we get the interval [0, π] as range of y  =  cot^-1(x).

Note : Starting point is 0.

Case 2 :

If we consider the first quadrant for positive and fourth quadrant for negative, we get the interval [-π/2, π/2] as range of

y  =  cot^-1(x).

Note : Starting point is -π/2.

When we consider the second case, we will get the interval [-π/2, π/2] as range of y  =  cot^-1(x).

But there is a value 0 in the interval [-π/2, π/2] for which we have                     

cot (0)  =  undefined

So we can not consider 0 as a part of the range of

y  =  cot^-1(x).

So we can ignore case 2 and consider case 1. 

When we consider case 1, we get the interval [0, π] as range of       

y  =  cot^-1(x)

Even though we get the interval [0, π] as range of

y  =  cot^-1(x),

cot x becomes undefined for the two corner values 0 and π.

So 0 and π can not be considered as parts of the range of

y  =  cot^-1(x).

So, the range of y  =  cot^-1(x) is

(0, π)

More clearly, the range of y  =  cot^-1(x) is,

0 < y < π

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.