DOMAIN AND RANGE OF A QUADRATIC FUNCTION

The general form of a quadratic function is

y  =  ax² + bx + c

Domain is all real values of x for which the given quadratic function is defined. 

Range is all real values of y for the given domain (real values values of x). 

Domain of a Quadratic Function

The general form a quadratic function is 

y  =  ax² + bx + c

The domain of any quadratic function in the above form is all real values. 

Because, in the above quadratic function, y is defined for all real values of x.  

Therefore, the domain of the quadratic function in the form y  =  ax² + bx + c is all real values. 

That is, 

Domain  =  {x | x ∈ R}

Range of a Quadratic Function

To know the range of a quadratic function in the form

y  =  ax² + bx + c,

we have to know the following two stuff. 

They are, 

(i) Parabola is open upward or downward

(ii) y-coordinate at the vertex of the Parabola .  

Let us see, how to know whether the graph (parabola) of the quadratic function is open upward or downward. 

(i) Parabola is open upward or downward :

y  =  ax² + bx + c

If the leading coefficient or the sign of "a" is positive, the parabola is open upward and "a" is negative, the parabola is open downward.  

(ii) y-coordinate at the vertex :

To know y - coordinate of the vertex, first we have to find the value "x" using the formula given below. 

x  =  -b/2a

Now, we have to plug x  =  -b/2a in the given quadratic function.

So, y - coordinate of the quadratic function is 

y  =  f(-b/2a)

How to find range from the above two stuff :

(i)  If the parabola is open upward, the range is all the real values greater than or equal to

y  =  f(-b/2a)

(i)  If the parabola is open downward, the range is all the real values less than or equal to

y  =  f(-b/2a)

Solved Problems

Problem 1 : 

Find the domain and range of the quadratic function given below. 

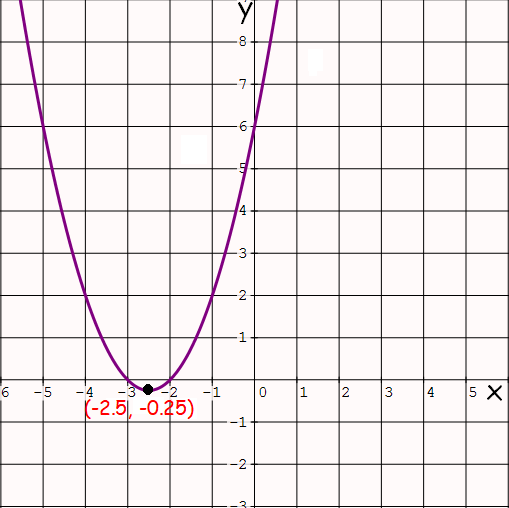
y  =  x² + 5x + 6

Solution :

Domain :

In the quadratic function, y  =  x² + 5x + 6, we can plug any real value for x. 

Because, y is defined for all real values of x.  

Therefore, the domain of the given quadratic function is all real values. 

That is, 

Domain  =  {x | x ∈ R}

Range : 

Comparing the given quadratic function y  =  x² + 5x + 6 with  

y  =  ax² + bx + c

we get 

a  =  1

b  =  5

c  =  6

Since the leading coefficient "a" is positive, the parabola is open upward.  

Find the x-coordinate at the vertex. 

x  =  -b / 2a

Substitute 1 for a and 5 for b.  

x  =  -5/2(1)

x  =  -5/2

x  =  -2.5

Substitute -2.5 for x in the given quadratic function to find y-coordinate at the vertex. 

y  =  (-2.5)² + 5(-2.5) + 6

y  =  6.25 - 12.5 + 6

y  =  - 0.25

So, y-coordinate of the vertex is -0.25

Because the parabola is open upward, range is all the real values greater than or equal to -0.25

Range  =  {y | y ≥ -0.25}

To have better understanding on domain and range of a quadratic function, let us look at the graph of the quadratic function y  =  x² + 5x + 6.

When we look at the graph, it is clear that x (Domain) can take any real value and y (Range) can take all real values greater than or equal to -0.25  

Problem 2 : 

Find the domain and range of the quadratic function given below. 

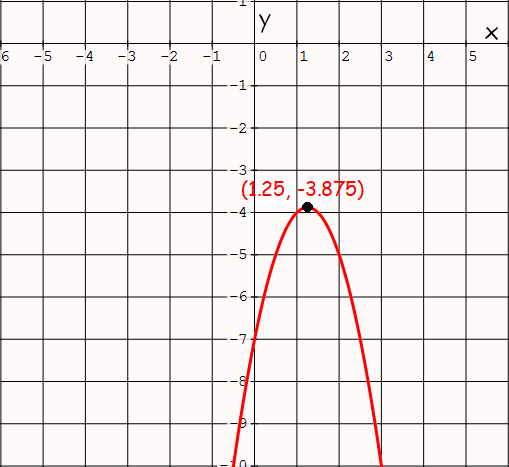
y  =  -2x² + 5x - 7

Solution :

Domain :

In the quadratic function, y  =  -2x² + 5x - 7, we can plug any real value for x. 

Because, y is defined for all real values of x  

Therefore, the domain of the given quadratic function is all real values. 

That is, 

Domain  =  {x | x ∈ R}

Range : 

Comparing the given quadratic function y  =  -2x² + 5x - 7 with 

y  =  ax² + bx + c

we get 

a  =  -2

b  =  5

c  =  -7

Since the leading coefficient "a" is negative, the parabola is open downward.  

x  =  -b / 2a

Substitute -2 for a and 5 for b.  

x  =  -5/2(-2)

x  =  -5/(-4)

x  =  5/4

x  =  1.25

Substitute 1.25 for x in the given quadratic function to find y-coordinate at the vertex. 

y  =  -2(1.25)² + 5(1.25) - 7

y  =  -3.125 + 6.25 - 7

y  =  -3.875

So, y-coordinate of the vertex is -3.875.

Because the parabola is open downward, range is all the real values greater than or equal to -3.875.

Range  =  {y | y ≤ -3.875}

To have better understanding on domain and range of a quadratic function, let us look at the graph of the quadratic function y  =  -2x² + 5x - 7.

When we look at the graph, it is clear that x (Domain) can take any real value and y (Range) can take all real values less than or equal to -3.875  

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.