DIVIDING POLYNOMIALS BY LONG DIVISION WORKSHEET

Divide the following polynomials using long division.

Problem 1 :

(2x³ - 6x² + 5x + 4) ÷ (x - 2)

Problem 2 :

(4x³ - 5x² + 6x - 2) ÷ (x - 1)

Problem 3 :

(x³ - 7x² - x + 6) ÷ (x + 2)

Problem 4 :

(10- 4x + 3x²) ÷ (x - 2)

Problem 5 :

f(x) = -2(x² + 7x - 3) - a(x + 2) + 1

In the polynomial f(x) is defined above, a is constant. IF f(x) is divisible by x, what is the value of a ?

a)  -5/2     b)  -3    c)  7/2   d)  5

Problem 6 :

If (-2x² + 5x + 10)/(-x + 4) = (2x + 3) - A/(-x + 4), what is the value of A ?

Problem 7 :

(x³ - x² + 3x - 3) ÷ (x - 1)

Which of the follwoing is the quotient of the expression above ?

a)  x² - 3      b)  x² + 3     c)  x² - 2x     d)  x² - 2x + 3

Problem 8 :

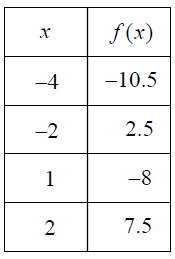
The function f is defined by a polynomial some values of x and f(x) are shown in the table above. What is the remainder when f(x) is divided by x + 2 ?

a)  -10.5     b)  -8     c)  2.5     d)  7.5

Problem 9 :

g(x) = -(x² - 6x + 5) - 4(x - c)

In the polynomial g(x) defined above, c is a constant. If g(x) is divisible by x + 1, what is the value of c ?

a)  1     b)  2    c)  3    d) 4

Problem 10 :

Which of the following is not a factor of the polynomial p(x) = 2x³ - 5x² - 4x + 3 ?

a)  2x - 1     b)  x + 1    c)  x - 3    d) x - 1

1. Answer :

(2x³ - 6x² + 5x + 4)  ÷  (x - 2)

Let P(x) = 2x³ - 6x² + 5x + 4 and g(x) = x - 2

To divide the given polynomial by x - 2, we have divide the first term of the polynomial P(x) by the first term of the polynomial g(x).

If we divide 2x³ by x, we get 2x². Now we have to multiply this 2x² by x - 2. From this we get 2x³ - 4x². 

Now we have to subtract 2x³ - 4x² from the given polynomial. So we get -2x² + 5x + 4.

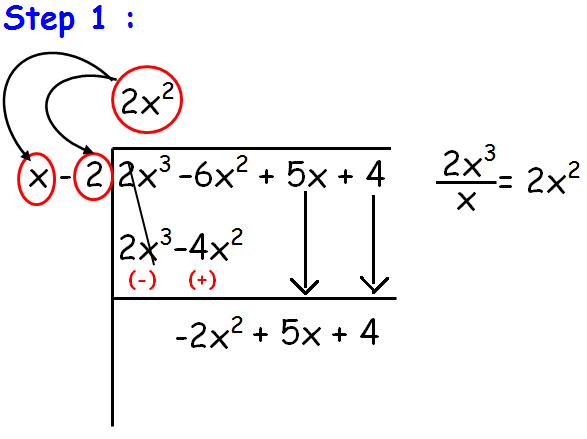
Now we have to subtract 2x³ - 4x² from the given polynomial. So we get -2x² + 5x + 4.

repeat this process until we get the degree of p(x) ≥ degree of g(x).

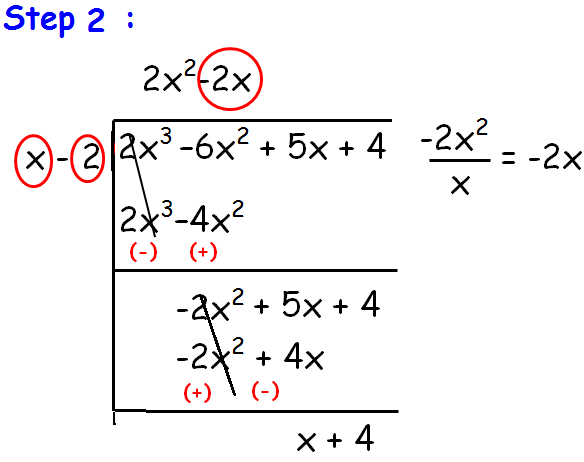
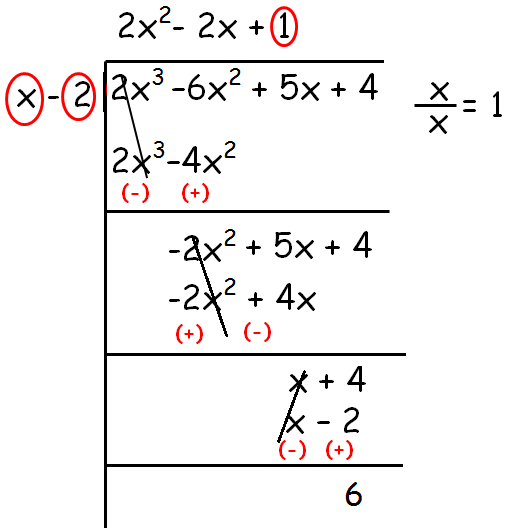
So,

Quotient  =  2x² - 2x + 1

Remainder = 6

2. Answer :

(4x³ - 5x² + 6x - 2)  ÷  (x - 1)

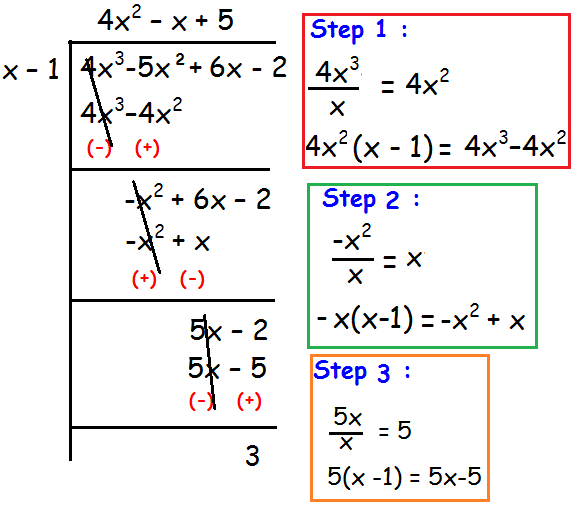
So,

Quotient  =  4x² - x + 5

Remainder  =  3

3. Answer :

(x³ - 7x² - x + 6)  ÷  (x + 2)

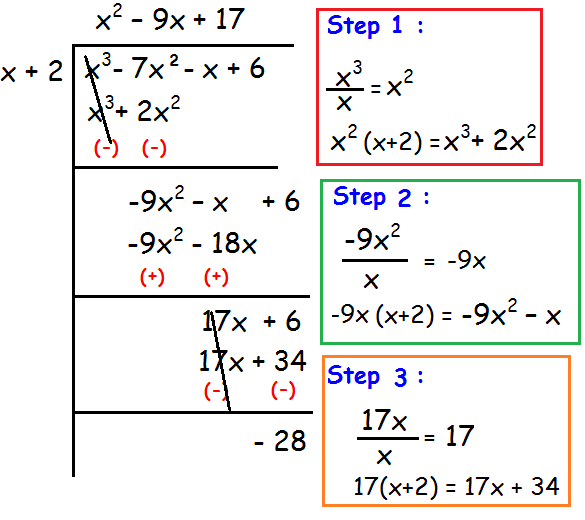
So, 

Quotient  =  x² - 9x + 17

Remainder  =  -28

4. Answer :

(10- 4x + 3x²)  ÷  (x - 2)

Let us first write the terms of each polynomial in descending order ( or ascending order).

Thus, the given problem becomes (10- 4x + 3x²) ÷ (x - 2)

f(x)  =  10- 4x + 3x²

=  3x² - 4x + 10

g(x) = x - 2  

Step 1 :

In the first step, we are going to divide the first term of the dividend by the first first term of the divisor.

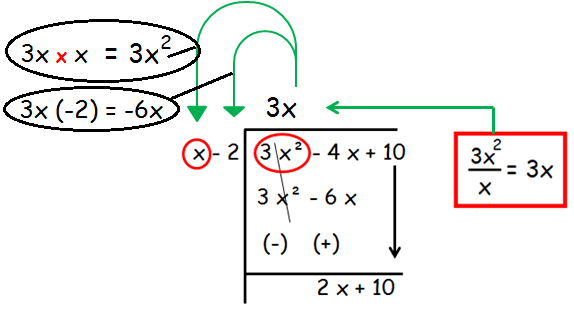
After changing the signs, +3x² and -3x² will get canceled. By simplifying, we get 2x + 10.

Step 2 :

In the second step again we are going to divide the first term that is 2x by the first term of divisor that is x.

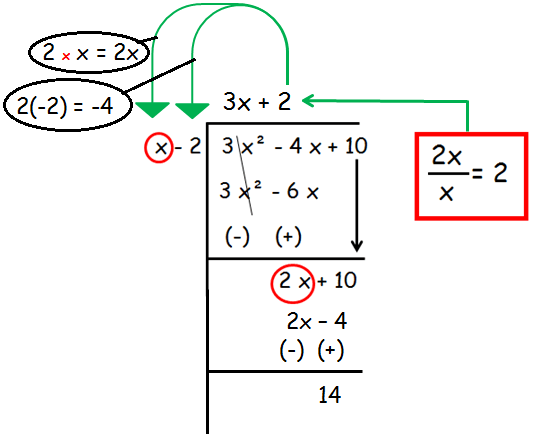
So,

Quotient  =  3x + 2

Remainder  =  14

5. Answer :

f(x) = -2(x² + 7x - 3) - a(x + 2) + 1

Since the polynomial is divisible by x, that is x - 0, we will get the remainder as 0.

We may solve this problem using remainder theorem.

f(0) = -2(0² + 7(0) - 3) - a(0 + 2) + 1

0 = -2(-3) - 2a + 1

0 = 6 - 2a + 1

0 = 7 - 2a

2a = 7

a = 7/2

So, the value of a is 7/2, otpion c is correct.

6. Answer :

If (-2x² + 5x + 10)/(-x + 4) = (2x + 3) - A/(-x + 4), what is the value of A ?

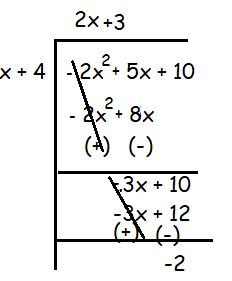
(2x + 3) - [2/(-x + 4)]

Comparing this with (2x + 3) - A/(-x + 4), the value of A is 2.

7. Answer :

(x³ - x² + 3x - 3) ÷ (x - 1)

Dividing the polynomial by the linear, 

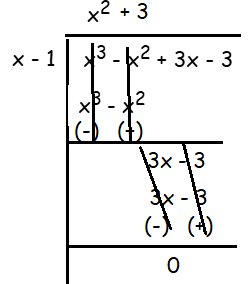
The required quotient is x² + 3.

8. Answer :

By observing the table, applying the value of x as -4, we get the remainder -10.5

Dividing the polynomial by x + 4, we get the remainder as -10.5

Dividing the polynomial by x + 2, we get the remainder as 2.5

So, option c is correct.

9. Answer :

g(x) = -(x² - 6x + 5) - 4(x - c)

Dividing the polynomial by x + 1, that is x + 1 = 0

x = -1

Applying -1 as x, we get

g(x) = -(x² - 6x + 5) - 4(x - c)

Since it is divisible by -1, we ge the remainder as 0

g(-1) =  -((-1)² - 6(-1) + 5) - 4(-1 - c)

0 = -(1 + 6 + 5) + 4 + 4c

0 = -12 + 4 + 4c

0 = -8 + 4c

4c = 8

c = 8/4

c = 2

So, the value of c is 2, option b is correct.

10. Answer :

p(x) = 2x³ - 5x² - 4x + 3

Dividing the polynomial by 2x + 1, 2x + 1 = 0

2x = -1

x = -1/2

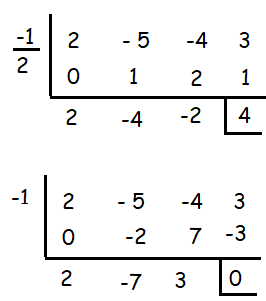
Dividing the polynomial by x + 1, we get the remainder 0. So, option b is correct.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.