DISTRIBUTIVE PROPERTY OF SET
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
For any two two sets, the following statements are true.
(i) Union distributes over intersection :
Au(BnC) = (AUB)n(AuC)
(ii) Intersection distributes over union
An(BuC) = (AnB)u(AnC)
Example 1 :
Given :
A = {0, 1, 2, 3, 4}
B = {1, -2, 3, 4, 5, 6}
C = {2, 4, 6, 7}
Show that
Au(BnC) = (AuB)n(AuC)
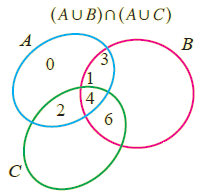
Also, verify the above using Venn diagram.
Solution :
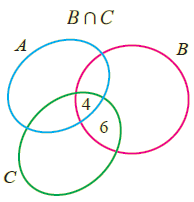
BnC = {1, -2, 3, 4, 5, 6} n {2, 4, 6, 7}.
BnC = {4, 6}
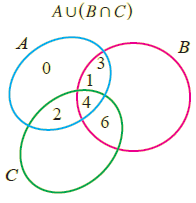
Au(BnC) = {0, 1, 2, 3, 4} u {4, 6}
Au(BnC) = {0, 1, 2, 3, 4, 6} -----(1)
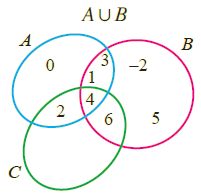
AuB = {0, 1, 2, 3, 4} u {1, - 2, 3, 4, 5, 6}
= {-2, 0, 1, 2, 3, 4, 5, 6}
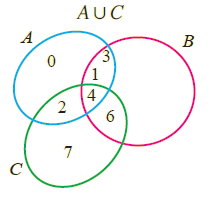
AuC = {0, 1, 2, 3, 4} u {2, 4, 6, 7}
= {0, 1, 2, 3, 4, 6, 7}
(AuB)n(AuC) = {-2, 0, 1, 2, 3, 4, 5, 6} n {0, 1, 2, 3, 4, 6, 7}
(AuB)n(AuC) = {0, 1, 2, 3, 4, 6} ----(2)
From (1) and (2),
Au(BnC) = (AuB)n(AuC)
Venn Diagram :
 |
 |
 |
 |
 |
Example 2 :
Given :
A = {x : - 3 ≤ x < 4, x ∊ R}
B = {x ; x < 5, x ∊ N}
C = {- 5, - 3, -1, 0, 1, 3}
Show that
A n (B u C) = (A n B) u (A n C)
Solution :
A = {x : - 3 ≤ x < 4, x ∊ R} ----> A = {-3, -2, -1, 0, 1, 2, 3}
B = {x ; x < 5, x ∊ N} ----> B = {1, 2, 3, 4}
C = {- 5, - 3, -1, 0, 1, 3}
B u C = {1, 2, 3, 4} u {- 5, - 3, - 1, 0, 1, 3}
B u C = {-5, -3, -1, 0, 1, 2, 3, 4}
A n (B u C) = {-3, -2, -1, 0, 1, 2, 3} n {-5, -3, -1, 0, 1, 2, 3, 4}
A n (B u C) = {-3, -1, 0, 1, 2, 3} ----(1)
A n B = {-3, -2, -1, 0, 1, 2, 3} n {1, 2, 3, 4}
A n B = {1, 2, 3}
A n C = {-3, -2, -1, 0, 1, 2, 3} n {- 5, - 3, - 1, 0, 1, 3}
A n C = {-3, -1, 0, 1, 2, 3}
(A n B) u (A n C) = {1, 2, 3} U {-3, -1, 0, 1, 2, 3}
(A n B) u (A n C) = {-3, -1, 0, 1, 2, 3} ----(2)
From (1) and (2),
A n (B u C) = (A n B) u (A n C)
Example 3 :
Using the Venn diagram shown, list the elements of each of the following sets :
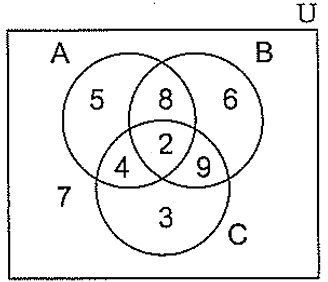
|
a) A\B b) A n B c) (AnB)\C |
d) AnBnC e) AUBUC f) (AUBUC)' |
Solution :
a) A\B
Leave the common elements of A and B, choose the remaining elements of A.
A\B = {5}
b) A n B
Write the common elements of the sets A and B.
A n B = {8, 2}
c) (A n B)\C
= {8, 2} \ {2, 4, 3, 9}
Leave the common elements and remaining elements of A n B
= {8}
d) AnBnC
Writing the common elements of the set A, B and C.
= {2}
e) AUBUC
Writing all elements in these three sets.
AUBUC = {2, 3, 4, 5, 6, 8, 9}
f) (AUBUC)'
U = {2, 3, 4, 5, 6, 7, 8, 9}
A U B U C = {2, 3, 4, 5, 6, 8, 9}
Leave the common elements in both sets and write the remaining elements U.
(AUBUC)' = {7}
Example 4 :
Let A = {k: k ∈ N, N ≤ 20}
B = {3k - 1, k ∈ N}
C = {2k + 1, k ∈ N}
Determing the sets
a) A n B n C
b) (A n B) \ C
c) (A n C) \ B
Solution :
Let A = {k: k ∈ N, N ≤ 20}
N is a natural number starts with 1.
A= {1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20}
B = {3k - 1, k ∈ N}
- When k = 1
- 3k - 1 = 3(1) - 1 ==> 2
- When k = 2
- 3k - 1 = 3(2) - 1 ==> 5
- When k = 3
- 3k - 1 = 3(3) - 1 ==> 8
- When k = 4
- 3k - 1 = 3(4) - 1 ==> 11
- When k = 5
- 3k - 1 = 3(5) - 1 ==> 14
- When k = 6
- 3k - 1 = 3(6) - 1 ==> 17
- When k = 7
- 3k - 1 = 3(7) - 1 ==> 20
B = {2, 5, 8, 11, 14, 17, 20}
C = {2k + 1, k ∈ N}
- When k = 1
- 2k + 1 = 2(1) + 1 ==> 3
- When k = 2
- 2k + 1 = 2(2) + 1 ==> 5
- When k = 3
- 2k + 1 = 2(3) + 1 ==> 7
- When k = 4
- 2k + 1 = 2(4) + 1 ==> 9
- When k = 5
- 2k + 1 = 2(5) + 1 ==> 11
- When k = 6
- 2k + 1 = 2(6) + 1 ==> 13
- When k = 7
- 2k + 1 = 2(7) + 1 ==> 15
- When k = 8
- 2k + 1 = 2(8) + 1 ==> 17
- When k = 9
- 2k + 1 = 2(9) + 1 ==> 19
C = {3, 5, 7, 9, 11, 13, 15, 17, 19}
a) A n B n C
Common elements in all three sets A, B and C.
= {5, 11, 17}
b) (A n B) \ C
(A n B) = {2, 5, 8, 11, 14, 17, 20}
(A n B) \ C = {2, 5, 8, 11, 14, 17, 20} \ {3, 5, 7, 9, 11, 13, 15, 17, 19}
= {2, 8, 14, 20}
c) (A n C) \ B
(A n C) = {3, 5, 7, 9, 11, 13, 15, 17, 19}
(A n C) \ B = {3, 5, 7, 9, 11, 13, 15, 17, 19} \ {2, 5, 8, 11, 14, 17, 20}
= {3, 7, 9, 13, 15, 19}
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
About Us | Contact Us | Privacy Policy
©All rights reserved. onlinemath4all.com

Recent Articles
-
Digital SAT Math Problems and Solutions (Part - 50)
Mar 06, 26 07:48 PM
Digital SAT Math Problems and Solutions (Part - 50) -
Digital SAT Math Problems and Solutions (Part - 49)
Mar 06, 26 06:47 PM
Digital SAT Math Problems and Solutions (Part - 49) -
Digital SAT Math Problems and Solutions (Part - 48)
Mar 06, 26 05:24 PM
Digital SAT Math Problems and Solutions (Part - 48)


