DIRECTION COSINES WORD PROBLEMS IN VECTORS

Problem 1 :

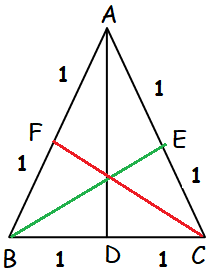
A triangle is formed by joining the points (1, 0, 0), (0, 1, 0) and (0, 0, 1). Find the direction cosines of the medians.

Solution :

Let the given points be A (1, 0, 0) B (0, 1, 0) and C (0, 0, 1)

OA vector  =  1i vector

OB vector  =  1j vector

OC vector  =  1k vector

AB vector  =  OB vector - OA vector

=  (j - i) vector

BC vector  =  OC vector - OB vector

=  (k - j) vector

CA vector  =  OA vector - OC vector

=  (i - k) vector

Problem 2 :

If 1/2, 1/√2, a are the direction cosines of some vector, then find a.

Solution :

Since the given are the direction ratios of some vector, it must satisfies the condition given below.

x²+ y² + z²  =  1

(1/2)²+ (1/√2)² + a²  =  1

(1/4) + (1/2)  + a²  =  1

a²  =  1 - (1/4) - (1/2)

a²  =  (4 - 1 - 1)/4  =  2/4  =  1/2

a  =  ±1/√2

Problem 3 :

If (a , a + b , a + b + c) is one set of direction ratios of the line joining (1, 0, 0) and (0, 1, 0), then find a set of values of a, b, c.

Solution :

Let the given points as A (1, 0, 0) and B (0, 1, 0)

OA = i vector and OB  = j vector

AB vector  =  OB vector - OA vector  =  j - i

Direction ratios of AB vector =  (-1, 1, 0)

By comparing the direction ratios with the given information, we get 

a  =  -1  ---(1)

a + b  =  1  ---(2)

a + b + c  =  0  ---(3)

By applying the value of a in (2), we get the value of b

-1 + b  =  1

b  =  1 + 1  =  2

By applying the values of a and b in (3), we get c.

-1 + 2 + c  =  0

1 + c  =  0

c  =  -1

So, the answer is (-1, 2, -1) (or) (1, -2, 1).

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.