DIFFERENT TYPES OF NUMBERS

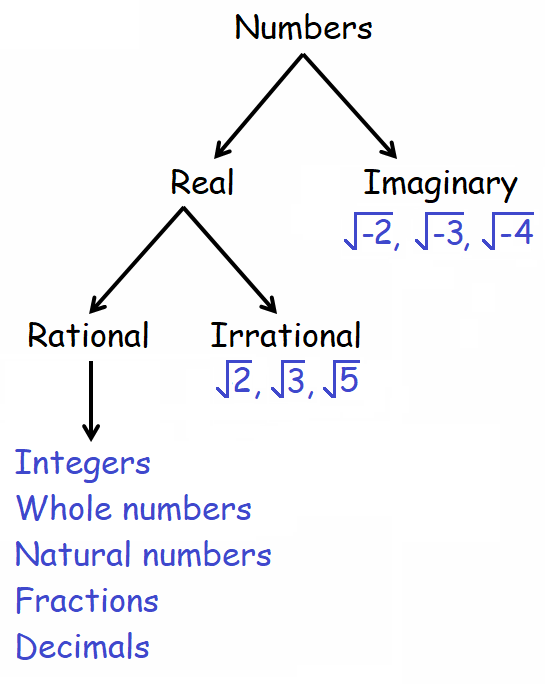
In Mathematics, we have different types of numbers. Initially, numbers can be broadly classified into two types. That is, real and imaginary numbers.

Real numbers can be further be classified into rational and irrational numbers. Rational numbers can further be classified into integers, whole numbers, natural numbers, fractions and  decimals.

Natural numbers :

Natural numbers or counting numbers are the most basic types of numbers you learned for the first time as toddlers. They start from 1 and go to infinity, i.e., 1, 2, 3, 4, 5, 6, and so on. They are also called positive integers. In the set form, they can be written as :

{1, 2, 3, 4, 5, ......}

Natural numbers are represented by the symbol N.

Whole numbers :

Whole numbers are the set of natural numbers, including zero. This means they start from 0 and go up to 1, 2, 3, and so on, that is

{0, 1, 2, 3, 4, 5, ......}

Whole numbers are represented by the symbol W.

Integers :

Integers are the set of all whole numbers and the negatives of natural numbers. They contain all the numbers which lie between negative infinity and positive infinity. They can be positive, zero, or negative but cannot be written in decimal or fraction. Integers can be written in set form as

{......., -3, -2, -1, 0, 1, 2, 3, .......}

We can say that all whole numbers and natural numbers are integers, but not all integers are natural numbers or whole numbers.

The symbol Z represents integers.

Fractions :

A fraction represents parts of a whole piece. It can be written in the form p/q, where both p and q are whole numbers, and q can never be equal to 0 (q ≠ 0). All fractions are rational numbers, but not all rational numbers are fractions.

¾, ½, ¼

Decimals :

In this type the numbers always containing point. If we multiply the decimal with 10,100, 1000 or 10000 like that the decimal will move from right side. The decimal point is helping us to keep track of where the ‘ones’ place is. That is placed to the right of ones’ place. When we move right from the decimal point, each number place is divided by the number "10".

........, -0.5, -0.25, 0, 0.25, 0.5, ........

Percentage :

Percentage is the way of representing the numbers in terms of fraction of 100. We can split the word "PERCENT" as "PER + CENT". That means per hundred. Usually, in examination marks scored by the students is represented as percentage. That is, how many marks the student has scored out of 100.

25/100 = 25%

Rational Numbers :

In our number system we are representing the rational number in the form of fraction like a/b.

1.5 = 3/2

Irrational Numbers :

An irrational number is any real number which cannot be expressed as a simple fraction or rational number. Π, √2 are some examples or irrational numbers.

Real Numbers :

All numbers including positive integers, negative integers, rational numbers, irrational numbers, are called real numbers.

It is usually denoted as ℝ

Complex Numbers :

Complex number is a combination of real and imaginary numbers. It is usually expressed in the form a + ib where a is the real number and b is the complex number.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.