DIFFERENT TYPES OF FUNCTIONS

The five types of functions are

(i) One to one or Injective function

(ii) Onto or Surjective function

(iii) One to one and onto or Bijective function

(iv) Into function

(iv) Constant function

(v) Identity function

Let us discuss the above different types of functions in detail.

One to One or Injective Function

Let f : A ----> B be a function.

The function f is called an one-one function, if it takes different elements of A into different elements of B.

That is, we say f is one-one.

In other words f is one-one if no element in B is associated with more than one element in A.

A one-one function is also called an Injective function.

The figure given below represents a one-one function.

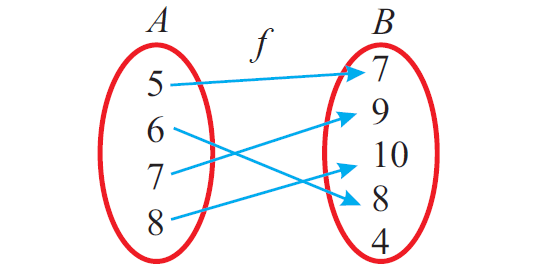
Onto or Surjective Function

Let f : A ----> B be a function.

The function f is called an onto function, if every element in B has a pre-image in A.

That is, in B all the elements will be involved in mapping. 

An onto function is also called a surjective function.

The figure given below represents a onto function.

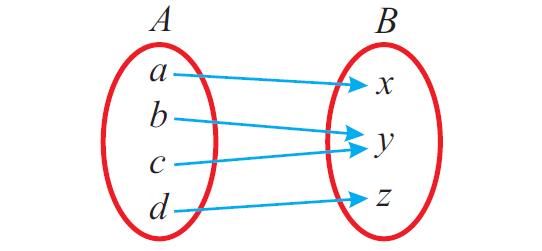
One to One and Onto or Bijective Function

Let f : A ----> B be a function.

The function f is called an one-one and onto or a bijective function if f is both a one-one and an onto function.

More clearly,

f maps distinct elements of A into distinct images in B and every element in B is an image of some element in A.

The figure given below represents a one to one and onto or bijective function.

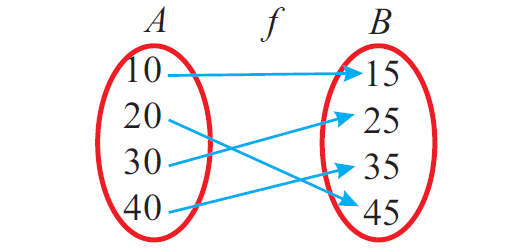
Into Function

Let f : A ----> B be a function.

The function f is called an into function, if there exists at least one element in B which does not have pre-image in A.

In other words, f is into, if the range of the function is a proper subset of co-domain B.

The figure given below represents a one-one function.

In the above mapping, the element '4' in B does not have pre-image in A.

Constant Function

The function f is called constant function if every element of A has the same image in B.

Range of a constant function is a singleton set.

Let A = {x, y, u, v, 1}, B = {3, 5, 7, 8, 10, 15}.

The function f : A ---> B defined by f (x) = 5 for every x belonging to A is a constant function.

The figure given below represents a constant function.

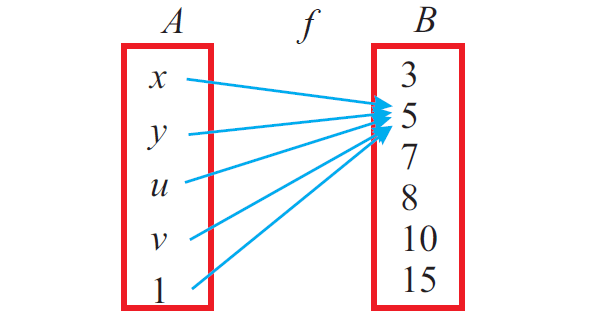
Identity Function

Let A be a non-empty set. A function f : A ---> A is called an identity function of A if f (a) = a for all a belonging to A.

That is, an identity function maps each element of A into itself.

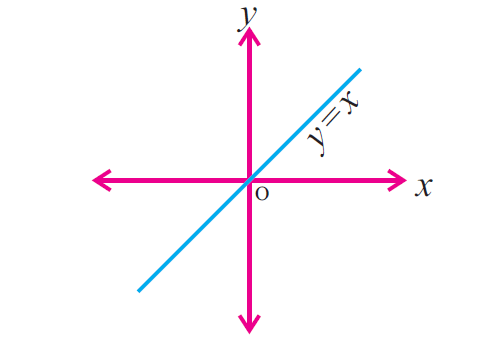
For example, let A be the set of real numbers (R). The function f : R ----> R be defined by f (x) = x for all x belonging to  R is the identity function on R.

The figure given below represents the graph of the identity function on R.

Terms Related to Functions 

Let f : A ----> B be a function.

Then, we have

Domain : Set A

Co-domain : Set B

Range : Elements of B involved in mapping.

Note :

In onto function, co-domain = Range.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.