DIFFERENCE BETWEEN INDUCTIVE AND DEDUCTIVE REASONING

Inductive and deductive reasoning are often confused. This section introduces the concept of reasoning and gives you tips and tricks to keeping inductive and deductive reasoning straight.

The following examples show how inductive and deductive reasoning differ.

(i) Lily knows that John is a sophomore and Michael is a junior. All the other juniors that Lily knows are older than John. Therefore, Lily reasons inductively that Michael is older than John based on past observations.

(ii) Lily knows that Michael is older than Chan. She also knows that Chan is older than John. Lily reasons deductively that Michael is older than John based on accepted statements.

Apart from the above two examples, let us look at the basic stuff of inductive reasoning and deductive reasoning separately to understand the difference between them better.

Inductive Reasoning

Looking for patterns and making conjectures is part of a process is called inductive reasoning.

It consists of three stages.

(i) Look for a pattern.

Look several examples. Use diagrams and tables to help to discover a pattern.

(ii) Make a conjecture.

Use the examples to make a general conjecture. A conjecture is an unproven statement that is based on observations. Discuss the conjecture with others. Modify the conjecture, if necessary.

(iii) Verify the conjecture.

Use logical reasoning to verify that the conjecture is true in all cases.

Deductive Reasoning

Deductive reasoning, unlike inductive reasoning, is a valid form of proof. It is, in fact, the way in which geometric  proofs are written. Deductive reasoning is the process by which a person makes conclusions based on previously known facts.

Deductive reasoning uses facts, definitions, and accepted properties in a logical order to write a logical statement.

Two Laws of Deductive Reasoning

(i) Law of detachment

(ii) Law of syllogism

Law of detachment :

If p -> q is a true conditional statement and p is true, then q is true.

Law of syllogism :

If p -> q and q -> p are true conditional statements, p->q is true.

Examples of Inductive Reasoning

Example 1 :

Sketch the next figure in the pattern.

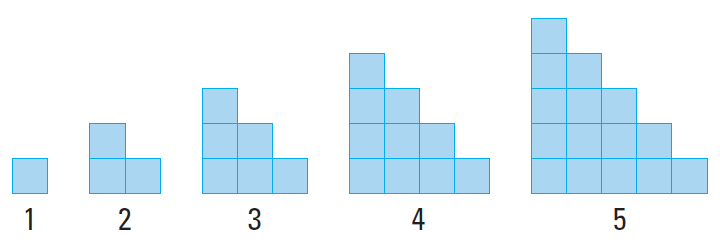
Solution :

Each figure in the pattern looks like the previous figure with another row of squares added to the bottom. Each figure looks like a stairway.

So, the sixth figure in the pattern must have six squares in the bottom row.

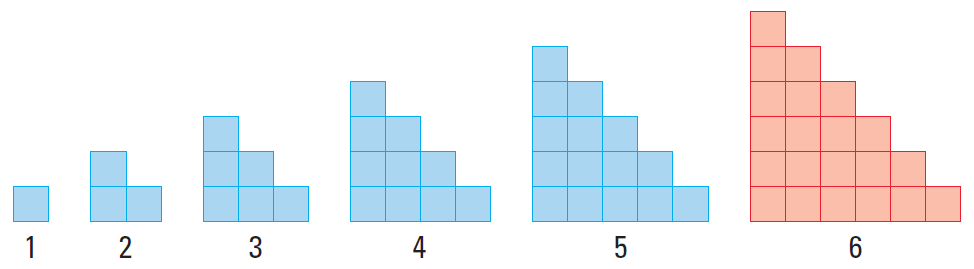
Example 2 :

Describe a pattern in the sequence of numbers. Predict the next number.

1, 4, 16, 64, ............

Solution :

Each number is four times the previous number.

So, the next number is 256.

Examples of Deductive Reasoning

Example 3 :

Let p be "the value of x is -5" and let q be "the absolute value of x is 5".

(i) Write p -> q in words.

(ii) Write q -> p in words.

(iii) Decide whether the biconditional statement p <-> q is true.

Solution :

(i) If the value of x is -5, then the absolute value of x is 5.

(ii) If the absolute value of x is 5, then the value of x is -5.

(iii) The conditional statement in part (a) is true, but its converse in part (b) is false. So, the biconditional statement p <-> q is false.

Example 4 :

State whether the argument is valid.

Michael knows that if he misses the practice the day before a game, then he will not be a starting player in the game. Michael misses practice on Tuesday so he concludes that he will not be able to start in the game on Wednesday.

Solution :

This logical argument is a valid use of the Law of Detachment. It is given that both a statement (p -> q) and its hypothesis (p) are true. So it is valid for Michael to conclude that the conclusion is true.

Example 5 :

Write some conditional statements that can be made from the following true statements using the Law of Syllogism.

1. If a bird is the fastest bird on land, then it is the largest of all birds.

2. If a bird is the largest of all birds, then it is an ostrich.

3. If a bird is a bee hummingbird, then it is the smallest of all birds.

4. If a bird is the largest of all birds, then it is flightless.

5. If a bird is the smallest bird, then it has a nest the size of a walnut half-shell.

Solution :

Here are the conditional statements that use the Law of Syllogism.

a. If a bird is the fastest bird on land, then it is an ostrich. (Use 1 and 2.)

b. If a bird is a bee hummingbird, then it has a nest the size of a walnut half-shell. (Use 3 and 5.)

c. If a bird is the fastest bird on land, then it is flightless. (Use 1 and 4.)

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.