DETERMINING ANGLE VISUALLY

In geometry, angles can be classified according to the size. There are five different types of angles. 

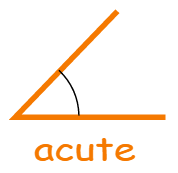
Acute angle

An angle that is less than 90°

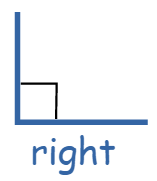
Right angle

An angle that is exactly 90°

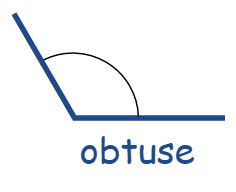
Obtuse angle

An angle that is greater than 90° but less than 180°

Straight angle

An angle that is exactly 180°

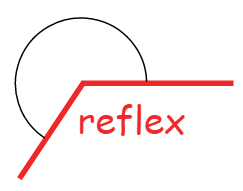
Reflex angle

An angle that is greater than 180° but less than 360°

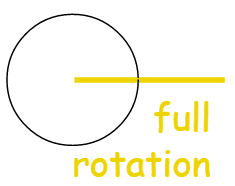
Full angle

An angle that is exactly 360°

Practice Problems

Problem 1 :

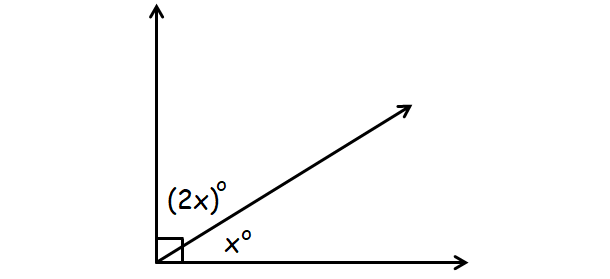
Find the value of x in the figure given below. 

Solution :

In the above diagram, x° and (2x)° together form a right angle.  

x° + (2x)° = 90°

x + 2x = 90

3x = 90

Divide each side by 3. 

x = 30°

Problem 2 :

Find the value of x in the figure given below. 

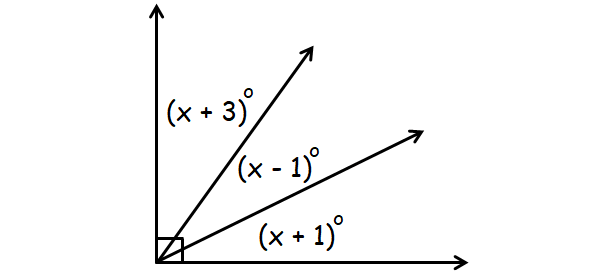
Solution :

In the diagram above, (x + 1), (x - 1) and (x + 3) together form a right angle.  

(x + 1) + (x - 1) + (x + 3) = 90°

x + 1 + x - 1 + x + 3 = 90

3x + 3 = 90

Subtract 3 from each side. 

3x = 87

Divide each side by 3.

x = 29

Problem 3 :

Find the value of x in the figure given below. 

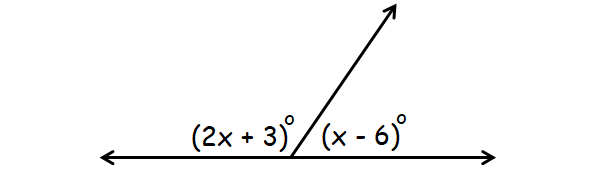
In the diagram above, (2x + 3)° and (x - 6)° together form a straight angle.  

(2x + 3)° + (x - 6)° = 180°

2x + 3 + x - 6 = 180

Simplify. 

3x - 3 = 180

Add 3 to each side. 

3x = 183

Divide each side by 3.

x = 61

Problem 4 :

Find the value of x in the figure given below. 

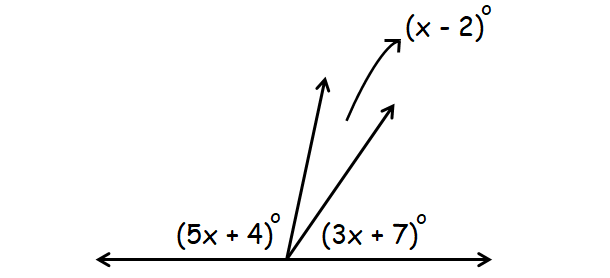
Solution :

In the diagram above, (5x + 4)°, (x - 2)° and (3x + 7)° together form a straight angle. 

(5x + 4)° + (x - 2)° + (3x + 7)° = 180°

5x + 4 + x -2 + 3x + 7 = 180

Simplify. 

9x + 9 = 180

Subtract 9 from each side.

9x = 171

Divide each side by 9. 

x = 19

Problem 5 :

Find the value of x in the figure given below. 

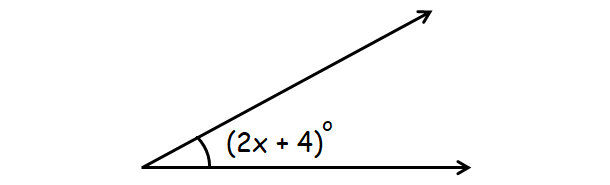
In the diagram above, (2x + 4)° is an acute angle. 

0° < (2x + 4)° < 90°

0 < 2x + 4 < 90

Subtract 4 from each value.  

-4 < 2x < 86

Divide each value by 2.

-2 < x < 43

Problem 6 :

Find the value of x in the figure given below. 

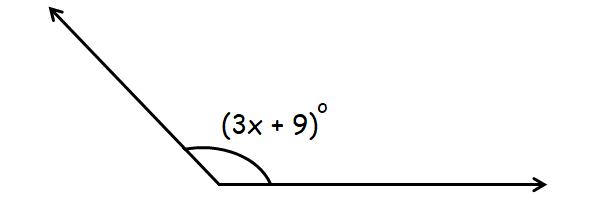
In the diagram above, (3x + 9)° is an obtuse angle. 

90° < (3x + 9)° < 180°

90 < 3x + 9 < 180

Subtract 9 from each value.  

81 < 3x < 171

Divide each value by 3.

27 < x < 57

Problem 7 :

Find the value of x in the figure given below. 

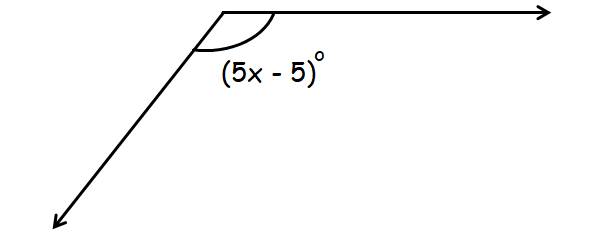
In the diagram above, (5x - 5)° is a reflex angle. 

180° < (5x - 5)° < 270°

180 < 5x - 5 < 270

Add 5 to each value.  

185 < 5x < 275

Divide each value by 5.

37 < x < 55

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.