DERIVING THE SLOPE INTERCEPT FORM OF AN EQUATION

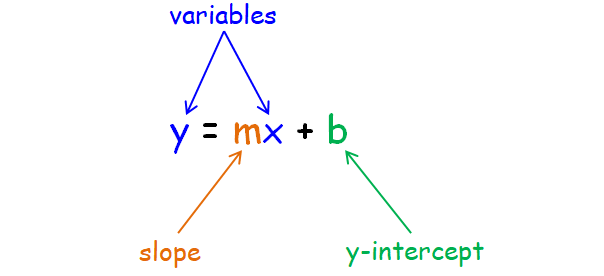
Equation of a straight line in slope-intercept form : 

y = mx + b

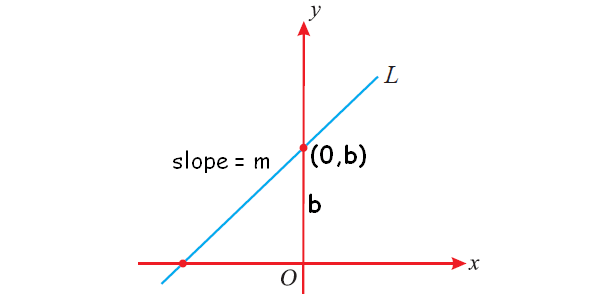
Let us see see, how to derive the slope-intercept form equation of a straight through the following steps.  

Step 1 :

Let L be a line with slope m and y-intercept b. Circle the point that must be on the line. Justify your choice.

(b, 0)   (0, b)   (0, m)   (m, 0)

The coordinate of x is 0 in the point that includes the y-intercept.

Step 2 :

Recall that slope is the ratio of change in y to change in x. Complete the equation for the slope m of the line using the y-intercept (0, b), and another point (x, y) on the line.

Slope m = change in y-values/change in x-values

Slope m = (y - b)/(x - 0)

Slope m = (y - b)/x

Step 3 :

In an equation of a line, we often want y by itself on one side of the equation. Solve the equation from Step 2 for y.

m = (y - b)/x

Multiply both sides by x

mx = [(y - b)/x]x

mx = y - b

Add b to both sides of the equation.

mx + b = (y - b) + b

mx + b = y

Write the equation with y on the left side.

y = mx + b

Reflect

Critical thinking : Write the equation of a line with slope m that passes  through the origin. Explain your reasoning.

y  =  mx

Because the origin is on the y-axis, the graph crosses the y-axis at (0, 0). So, the y-intercept b is 0, and y  =  mx + b becomes y  =  mx.

©All rights reserved. onlinemath4all.com