DEPENDENT SYSTEM OF LINEAR EQUATIONS

A system of linear equations is consistent and has infinitely many solutions is called dependent system.

So, all dependednt systems are always consistent and they have infinitely many solutions.

There are several ways to identify a dependent system of linear equations without graphing the lines.

We can also determine a dependent system of linear equation, if one equation is a multiple of the other.

When you graph a dependent system of linear equations in two variables, the lines will coincide. That is, the two lines will touch each other in all the points. Hence, the system is consistent and it has infinitely many solutions.

Graph of a dependent system of linear equations in two variables :

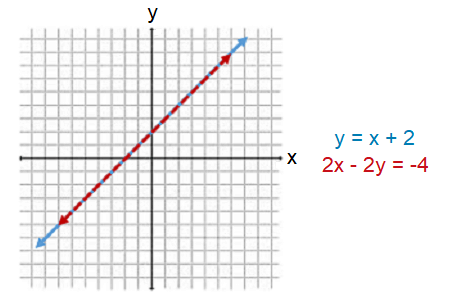
Solved Problems

In each case, check if the system of linear equations is dependent system.

Problem 1 :

2x + 3y - 5 = 0

4x + 6y - 10 = 0

Solution :

2x + 3y - 5 = 0 ----A

4x + 6y - 10 = 0 ----B

Both the given linear equations are in general form.

In B, the coefficient of x, coefficient of y and the constant term, all are multiple of 2. So, divide both sides of B by 2.

⁽⁴ˣ ⁺ ⁶ʸ ⁻ ¹⁰⁾⁄₂ = ⁰⁄₂

⁴ˣ⁄₂ ⁺ ⁶ʸ⁄₂ ⁻ ¹⁰⁄₂ = 0

2x + 3y - 5 = 0 ----(3)

Both A and C are in general form.

In A and C, the coefficients of x (2), the coefficients of y (3) and the constant terms (-5) are equal.

Therefore, the given system of linear equations is dependent system.

Problem 2 :

0.5x - 0.3y = 0.7

5x - 3y = 7

Solution :

0.5x - 0.3y = 0.7 ----A

5x - 3y = 7 ----B

Both the given linear equations are in standard form.

In A, the coefficient of x, coefficient of y and the constant term, all are decimals with one digit to the right of the decimal point. To get rid of the decimal point, multiply both sides of A by 10.

10(0.5x - 0.3y) = 10(0.7)

10(0.5x) + 10(-0.3y) = 7

5x - 3y = 7 ----C

Both B and C are in standard form.

In B and C, the coefficients of x (5), the coefficients of y (-3) and the constant terms (7) on right side are equal.

Therefore, the given system of linear equations is dependent system.

Problem 3 :

7x + 5y + 3 = 0

21x + 15y + 18 = 0

Solution :

7x + 5y + 3 = 0 ----A

21x + 15y + 18 = 0 ----B

Both the given linear equations are in general form.

Divide both sides of B by 3.

⁽²¹ˣ ⁺ ¹⁵ʸ ⁺ ¹⁸⁾⁄₃ = ↉

²¹ˣ⁄₃ ⁺ ¹⁵ʸ⁄₃ ⁺ ¹⁸⁄₃ = 0

7x + 5y + 6 = 0 ----C

Both A and C are in general form.

In A and C, the coefficients of x (7) and the coefficients of y (5) are equal. But, the constant terms are not equal.

3 ≠ 6

Therefore, the given system of linear equations is NOT dependent system.

Problem 4 :

0.2x - 0.1y = 0.9

2x - y = 19

Solution :

0.2x - 0.1y = 0.9 ----A

2x - y = 19 ----B

Both the given linear equations are in standard form.

Multiply both sides of A by 10 to get rid of the decimal point in each term.

10(0.2x - 0.1y) = 10(0.9)

10(0.2x) + 10(-0.1y) = 9

2x - y = 9 ----C

Both B and C are in standard form.

In B and C, the coefficients of x (2) and the coefficients of y (-1) are equal. But, the constant terms on the right side are not equal.

9 ≠ 19

Therefore, the given system of linear equations is NOT dependent system.

Problem 5 :

y = x + 2

2x - 2y = -4

Solution :

y = x + 2 ----A

2x - 2y = -4 ----B

A is in slope intercept form and B is in standard form.

Identify the slope (m) and y-intercept (b) in A.

Comparing y = mx + b and y = x + 2, we get

slope (m) = 1

y-intercept (b) = 2

To check, whether the given system of linear equations is dependent system, both the linear equation must be in the same form.

Since A is in slope-intercept form, write B also in slope-intercept form.

2x - 2y = -4

Divide both sides by 2.

⁽²ˣ ⁻ ²ʸ⁾⁄₂ = ⁻⁴⁄₂

²ˣ⁄₂ ⁻ ²ʸ⁄₂ = -2

x - y = -2

Subtract x from both sides.

(x - y) - x = -2 - x

x - y - x = -x - 2

-y = -x - 2

Multiply both sides by -1.

-1(-y) = -1(-x - 2)

y = -1(-x) - 1(-2)

y = x + 2 ----C

slope (m) = 1

y-intercept (b) = 2

Both A and C are in slope-intercept form.

In A and C, the slopes (1) and y-intercepts (2) are equal

Therefore, the given system of linear equations is dependent system.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.