DEPENDENT PAIR OF LINEAR EQUATIONS WORKSHEET

Question 1 :

Is a dependent pair of linear equations always consistent? Explain.

Question 2 :

How many solutions does a dependent pair of linear equations have?

Questions 3-6 : Check if the given pair of linear equations is a dependent pair of linear equations..

Question 3 :

3x + 5y - 6 = 0

9x + 15y - 18 = 0

Question 4 :

0.6x - 0.8y = 1.2

3x - 4y = 6

Question 5 :

x + 2y + 3 = 0

5x + 10y + 20 = 0

Question 6 :

0.7x - 0.2y = 0.5

7x - 2y = 25

Question 7 :

Check whether the following pair of linear equations is a dependent pair of linear equations graphically. 

y = x + 2

2x - 2y = -4

Answers

1. Answer :

Yes, a dependent pair of linear equations is always consistent. Because, both the lines in a dependent system will coincide or touch each other in all the points.

1. Answer :

Always, both the lines in a dependent pair of linear equations touch each other in all the points. So, a dependent pair of linear equations always has infinitely many solutions.

3. Answer :

3x + 5y - 6 = 0 ----P

9x + 15y - 18 = 0 ----Q

Both the given linear equations are in general form.

In Q, the coefficient of x, coefficient of y and the constant term, all are multiple of 3. So, divide both sides of Q by 2.

⁽⁹ˣ ⁺ ¹⁵ʸ ⁻ ¹⁸⁾⁄₃ = ⁰⁄₃

⁹ˣ⁄₃ ⁺ ¹⁵ʸ⁄₃ ⁻ ¹⁸⁄₃ = 0

3x + 5y - 6 = 0 ----R

Both P and R are in general form.

In P and R, the coefficients of x (3), the coefficients of y (5) and the constant terms (-6) are equal.

Therefore, the given pair of linear equations is a dependent pair of linear equations.

4. Answer :

0.6x - 0.8y = 1.2 ----P

3x - 4y = 6 ----Q

Both the given linear equations are in standard form.

In P, the coefficient of x, coefficient of y and the constant term, all are decimals with one digit to the right of the decimal point. To get rid of the decimal point, multiply both sides of P by 10.

10(0.6x - 0.8y) = 10(1.2)

10(0.6x) + 10(-0.8y) = 12

6x - 8y = 12

Divide both sides by 2.

⁽⁶ˣ ⁻ ⁸ʸ⁾⁄₂ = ¹²⁄₂

⁽⁶ˣ ⁻ ⁸ʸ⁾⁄₂ = 6

⁶ˣ⁄₂ ⁻ ⁸ʸ⁄₂ = 6

3x - 4y = 6 ----R

Both Q and R are in standard form.

In R and Q, the coefficients of x (3), the coefficients of y (-4) and the constant terms (6) on the right side are equal.

Therefore, the given pair of linear equations is a dependent pair of linear equations.

5. Answer :

x + 2y + 3 = 0 ----P

5x + 10y + 20 = 0 ----Q

Both the given linear equations are in general form.

Divide both sides of Q by 5.

⁽⁵ˣ ⁺ ¹⁰ʸ ⁺ ²⁰⁾⁄₅ = ⁰⁄₅

⁵ˣ⁄₅ ⁺ ¹⁰ʸ⁄₅ ⁺ ²⁰⁄₅ = 0

x + 2y + 4 = 0 ----R

Both P and R are in general form.

In P and R, the coefficients of x (1) and the coefficients of y (2) are equal. But, the constant terms are not equal.

3 ≠ 4

Therefore, the given pair of linear equations is NOT a dependent pair of linear equations.

6. Answer :

0.7x - 0.2y = 0.5 ----P

7x - 2y = 25 ----Q

Both the given linear equations are in standard form.

Multiply both sides of P by 10 to get rid of the decimal point in each term.

10(0.7x - 0.2y) = 10(0.5)

10(0.7x) + 10(-0.2y) = 5

7x - 2y = 5 ----R

Both Q and R are in standard form.

In Q and R, the coefficients of x (7) and the coefficients of y (-2) are equal. But, the constant terms on the right side are not equal.

25 ≠ 5

Therefore, the given pair of linear equations is NOT a dependent pair of linear equations.

7. Answer :

y = x + 2

2x - 2y = -4

The first one is in slope-intercept form and the second one is in standard form.

Graphing the first line y = x + 2 :

Identify the slope (m) and y-intercept of y = x + 2.

Comparing y = mx + b and y = x + 2, we get

slope (m) = 1

y-intercept (b) = 2

Using the slope (1) and y-intercept (2), graph the first line y = x + 2 in the xy-plane.

Graphing the first line 2x - 2y = -4 :

Take multiple values for x in 2x - 2y = -4 and find the corresponding values of y in the second linear equation. Then, write them as points in the form (x, y).

When x = -2,

2(-2) - 2y = -4

-4 - 2y = -4

-2y = 0

y = 0

(-2, 0)

When x = -2,

2(-2) - 2y = -4

-4 - 2y = -4

-2y = 0

y = 0

(-2, 0)

When x = -1,

2(-1) - 2y = -4

-2 - 2y = -4

-2y = -2

y = 1

(-1, 1)

When x = 0,

2(0) - 2y = -4

0 - 2y = -4

-2y = -4

y = 2

(0, 2)

When x = 1,

2(1) - 2y = -4

2 - 2y = -4

-2y = -6

y = 3

(1, 3)

When x = 2,

2(2) - 2y = -4

4 - 2y = -4

-2y = -8

y = 4

(1, 4)

Plot the following points in the xy-plane and connect them to get the graph of the second line 2x - 2y = -4.

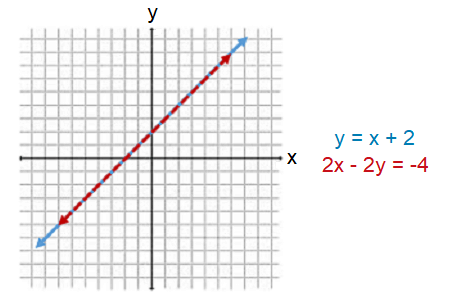
In the xy-plane above, the two lines coincide or they touch each other in all the points. So, the given pair of linear equations is consistent and it has infinitely many solutions.

Therefore, the given pair of linear equations is a dependent pair of linear equations.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.