DEFINITIONS AND BICONDITIONAL STATEMENTS

All definitions can be interpreted "forward" and "backward". For instance, the definition of perpendicular lines means.

(i) If two lines are perpendicular, then they intersect to form a right angle.

and

(ii) If two lines intersect to form a right angle, then they are perpendicular.

Conditional statements are not always written in if-then form. Another common form of a conditional statement is only-if-form.

Here is an example.

We can rewrite this conditional statement in if-then form as follows :

If it is Sunday, then I am in park.

A biconditional statement is a statement that contains the phrase "if and only if". Writing biconditional statement is equivalent to writing a conditional statement and its converse.

A biconditional statement can be either true or false. To be true, both the conditional statement and its converse must be true. This means that a true biconditional statement is true both “forward” and “backward.” All definitions can be written as true biconditional statements.

Example 1 :

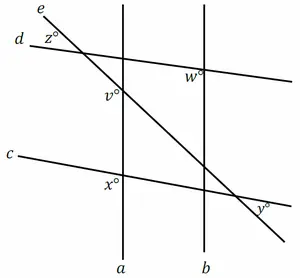
Whether each statement about the diagram is true. Explain your answer using the definitions you have learned.

(i) Points D, X and B are collinear.

(ii) AC is perpendicular to DB.

(iii) ∠AXB is adjacent to ∠CXD.

Solution :

(i) This statement is true. Two or more points are collinear, if they lie on the same line. The points D, X and B all lie on line DB. So they are collinear.

(ii) This statement is true. The right angle symbol in the diagram indicates that the lines AC and BD intersect to form a right angle. So, the lines are perpendicular.

(iii) This statement is false. By definition, adjacent angles must share a common side. Because ∠AXB and ∠CXD do not share a common side, they are adjacent.

Example 2 :

Write the following biconditional statement as a conditional statement and its converse.

"Three lines are coplanar if and only if they lie in the same plane"

Solution :

Conditional Statement:

If three lines are coplanar, then they lie in the same plane.

Converse:

If three lines lie in the same plane, then they are coplanar.

Example 3 :

Consider the following statement :

x = 3 if and only if x² = 9

(i) Is this a biconditional statement?

(ii) Is the statement true?

Solution :

(i) The statement is biconditional because it contains “if and only if.”

(ii) The statement can be rewritten as the following statement and its converse.

Conditional statement :

If x = 3, then x² = 9.

Converse :

If x² = 9, then x = 3.

The first of these statements is true, but the second is false. Because, if x² = 9, then x = 3 or -3.

So, the biconditional statement is false.

Example 4 :

Each of the following statements is true. Write the converse of each statement and decide whether the converse is true or false. If the converse is true, combine it with the original statement to form a true biconditional statement. If the converse is false, state a counterexample.

(i) If two points lie in a plane, then the line containing them lies in the plane.

(ii) If a number ends in 0, then the number is divisible by 5.

Solution :

Solution (i) :

Converse :

(i) If a line containing two points lies in a plane, then the points lie in the plane.

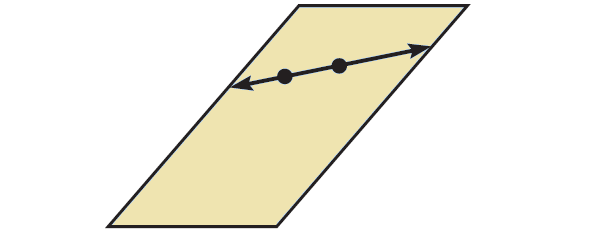
The converse is true, as shown in the diagram. So, it can be combined with the original statement to form the true biconditional statement written below.

Biconditional statement :

Two points lie in a plane, if and only if the line containing them lies in the plane.

Solution (ii) :

Converse :

If a number is divisible by 5, then the number ends in 0. The  converse is false. As a counterexample, consider the number 15. It is divisible by 5, but it does not end in 0, as shown below.

20 ÷ 5  =  4

25 ÷ 5  =  5

30 ÷ 5  =  6

Note :

Knowing how to use true biconditional statement is an important tool for reasoning in geometry. For instance, if you can write a true biconditional statement, then you can use the conditional statement or the converse to justify an argument.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.