DEFINE INTEGRALS
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Example 1 :
Evaluate the following
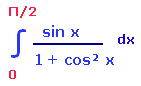
Solution :
Let t = cos x
Differentiating both sides with respect to x
dt = -sin x dx and sin x dx = -dt
We have changed the given function in terms of t from the variable x .So, we need to change the limits also.
|
When x = 0 t = cos 0 t = 1 |
When x = Π/2 t = cos Π/2 t = 0 |

Example 2 :
Evaluate the following
Integral 0 to Π/2 sin² x
Solution :
To solve this problem we have to use the trigonometric formula for sin² x.
sin²x = (1 - cos 2x)/2
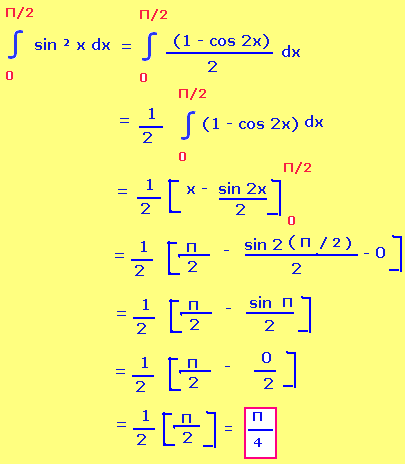
Example 3 :
Evaluate the following
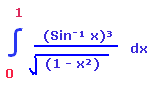
Solution :
t = Sin⁻¹x
Differentiating with respect to x on both sides
dt = 1/√(1-x²) dx
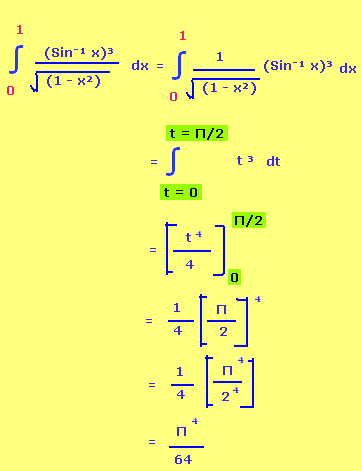
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
About Us | Contact Us | Privacy Policy
©All rights reserved. onlinemath4all.com

Recent Articles
-
10 Hard SAT Math Questions (Part - 42)
Dec 30, 25 05:52 AM
10 Hard SAT Math Questions (Part - 42) -
10 Hard SAT Math Questions (Part - 38)
Dec 29, 25 04:21 AM
10 Hard SAT Math Questions (Part - 38) -
10 Hard SAT Math Questions (Part - 39)
Dec 28, 25 11:20 PM
10 Hard SAT Math Questions (Part - 39)
