DEFINITE INTEGRAL USING CHANGE OF VARAIBLES

Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.

Problem 1 :

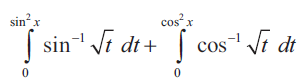
Solution :

Let t = sin²u

dt = 2 sinu cosu

dt = sin 2u du

Let t = cos²u

dt = 2 cosu (-sinu)

dt = -sin 2u du

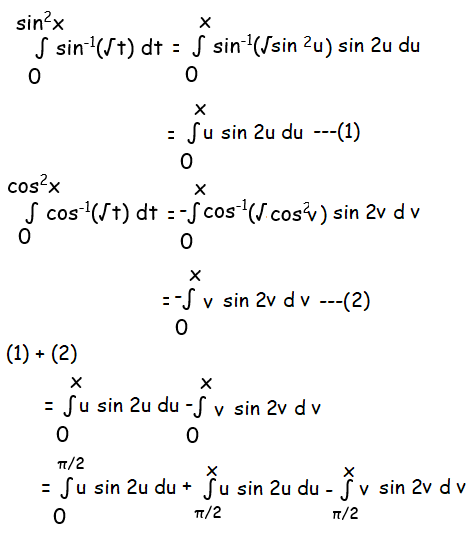
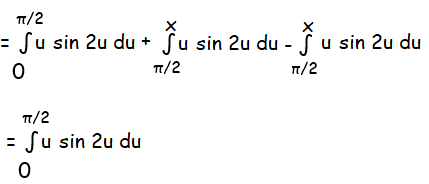
Using partial derivative, we get

u = u, du = du, dv = sin 2u ==> v = -cos 2u/2

∫udv = uv-∫vdu

= u(-cos 2u/2)-∫(-cos 2u/2) du

= u(-cos 2u/2)+(sin 2u/4)

By applying the limits, we get

= π/2((-cosπ)/2)) + (sinπ)/4

= π/2(1/2) + 0

= π/4

Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.

Recent Articles