DEFINITE INTEGRAL OF ABSOLUTE VALUE FUNCTIONS

Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.

The function involving the sign | | is known as modulus function.

Let us take a modulus function f(x) = |x|,

f(x) = x, when x > 0

f(x) = 0, when x = 0

Step 1 :

To evaluate the integral, we first equate the given function to zero and find x intercept.

Step 2 :

The modulus function will always have the shape of V. Draw the graph.

Step 3 :

With the given interval, divide the integral into parts, then integrate it.

Problem 1 :

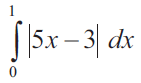
Solution :

Let y = 5x-3

put y = 0

5x-3 = 0

x = 3/5

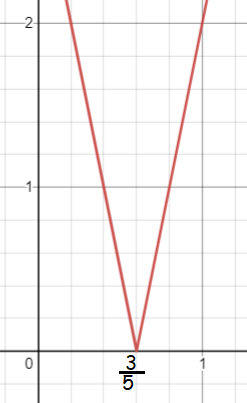
f(x) = -(5x-3), when x < 3/5

f(x) = (5x-3), when x > 3/5

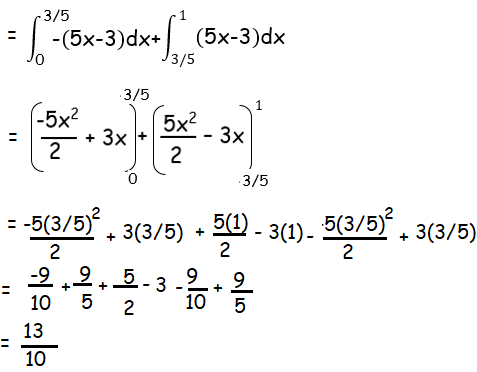
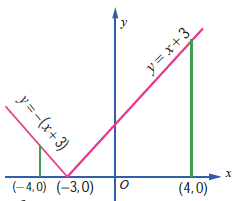
Problem 2 :

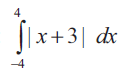
Solution :

Let y = x+3

put y = 0

x+3 = 0

x = -3

f(x) = -(x+3), when x < -3

f(x) = (x+3), when x > -3

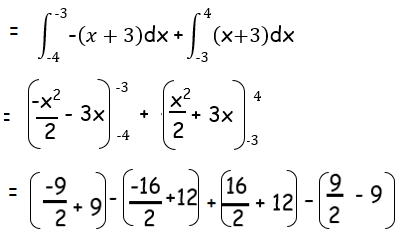
By simplifying, we get

= 25

So, the answer is 25.

Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.

Recent Articles