INCREASING AND DECREASING FUNCTIONS
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
To know whether a function is increasing or decreasing, we have to know where the graph of a function rises and where it falls. The graph shown below rises, falls, then rises again as we move from left to right:
It rises from A to B, falls from B to C, and rises again from C to D. The function f is said to be increasing when its graph rises and decreasing when its graph falls
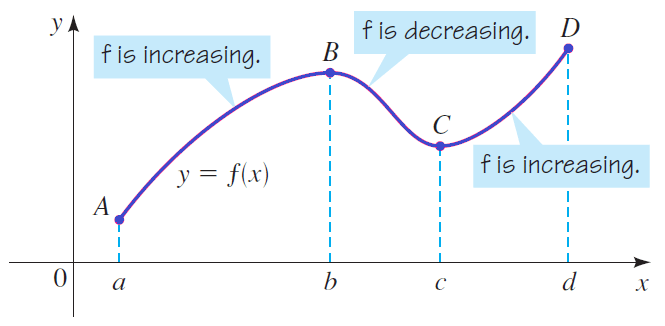
In the above graph,
f is increasing on [a, b] and [c, d]
f is decreasing on [b, c]
Increasing and Decreasing Functions
Increasing Function :
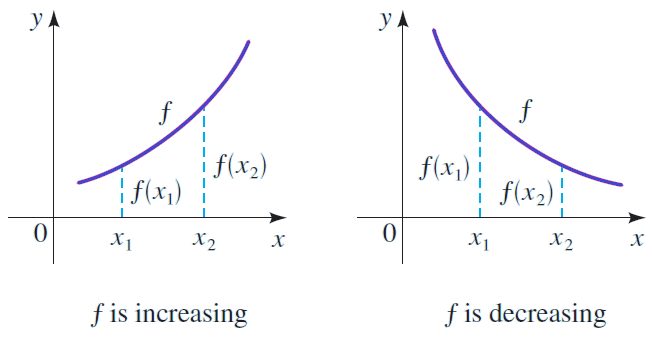
A function f is called increasing on an interval I, if
f(x1) ≤ f(x2)
whenever x1 < x2 in I.
Decreasing Function :
A function f is called decreasing on an interval I, if
f(x1) ≥ f(x2)
whenever x1 < x2 in I.
Strictly Increasing Function :
A function f is called strctly increasing on an interval I, if
f(x1) < f(x2)
whenever x1 < x2 in I.
Decreasing Function :
A function f is called strictly decreasing on an interval I, if
f(x1) > f(x2)
whenever x1 < x2 in I.
Using Derivative
Let I be an open interval. Let f : I -> R be differentiable.
Then
(i) f is increasing if and only if f'(x) ≥ 0 for all x in I.
(ii) f is decreasing if and only if f'(x) ≤ 0 for all x in I.
Example 1 :
The graph shown below gives the weight W of a person at age x. Determine the intervals on which the function W is increasing and on which it is decreasing.
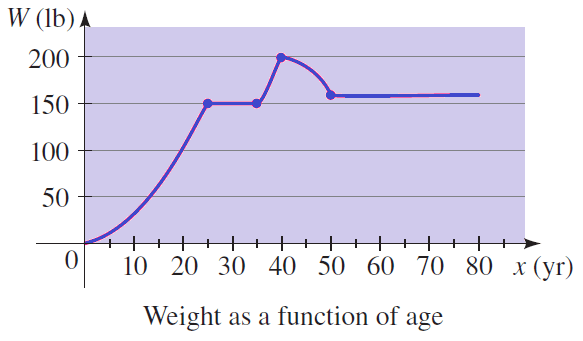
Solution :
The function is increasing on [0, 25] and [35, 40]. It is decreasing on [40, 50]. The function is constant (neither increasing nor decreasing) on [25, 35] and [50, 80]. This means that the person gained weight until age 25, then gained weight again between ages 35 and 40. He lost weight between ages 40 and 50.
Example 2 :
(a) Sketch the graph of the function f(x) = x2/3.
(b) Find the domain and range of the function.
(c) Find the intervals on which f increases and decreases.
Solution :
(a) We can use a graphing calculator to sketch the graph shown below.
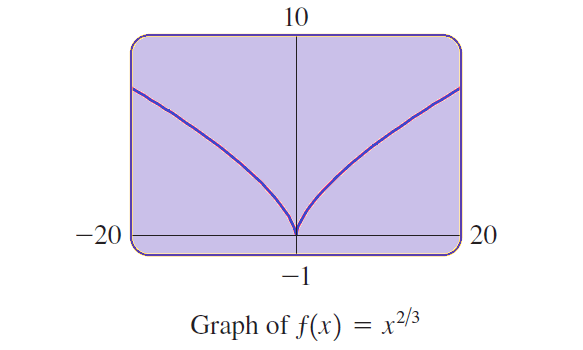
From the graph above, we can observer that
(b) the domain of f is R and the range is [0, ∞).
(c) f is decreasing on (-∞, 0] and increasing on [0, ∞).
Example 3 :
The graph of the function shown below has domain [−1, 6].
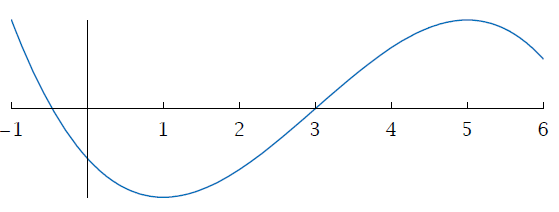
(a) Find the largest interval on which f is increasing.
(b) Find the largest interval on which f is decreasing.
(c) Find the largest interval containing 6 on which f is decreasing.
Solution :
From the graph above, we can observe,
(a) [1, 5] is the largest interval on which f is increasing.
(b) [−1, 1] is the largest interval on which f is decreasing.
(c) [5, 6] is the largest interval containing 6 on which f is decreasing.
Example 4 :
Shown below are the graphs of three functions; each function is graphed on its entire domain.
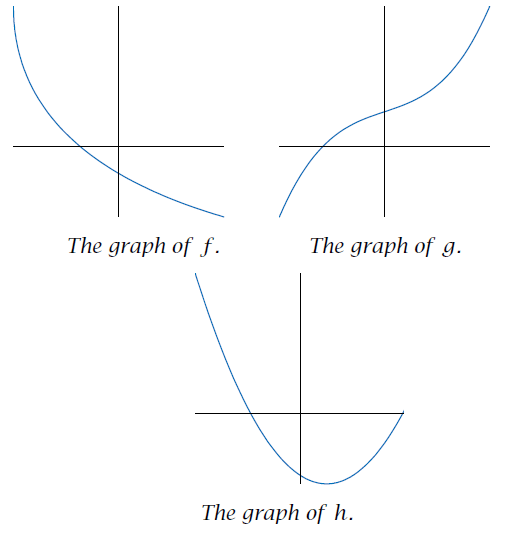
(a) Is f increasing, decreasing, or neither?
(b) Is g increasing, decreasing, or neither?
(c) Is h increasing, decreasing, or neither?
Solution :
(a) The graph of f gets lower from left to right on its entire domain. Thus f is decreasing.
(b) The graph of g gets higher from left to right on its entire domain. Thus g is increasing.
(c) The graph of h gets lower from left to right on part of its domain and gets higher from left to right on another part of its domain. Thus h is neither increasing nor decreasing.
Example 5 :
Here f has domain [0, 4] and g has domain [−1, 5].
(i) What is the largest interval contained in the domain of f on which f is increasing?
(ii) What is the largest interval contained in the domain of g on which g is increasing?
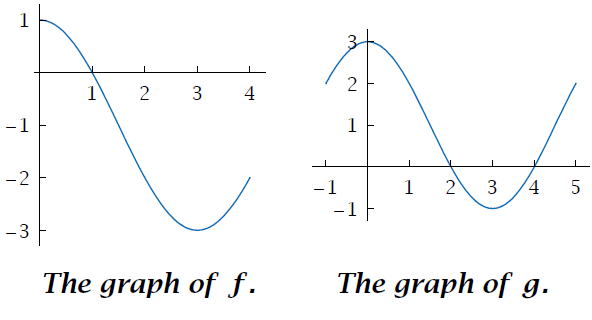
Solution :
(i) The largest interval on which the function f increasing is [3, 4].
(i) The largest interval on which the function g decreasing is [0, 3].
Example 6 :
Find the intervals in which f(x) = 2x3 + x2 - 20x is increasing and decreasing.
Solution :
f(x) = 2x3 + x2 - 20x
f'(x) = 6x2 + 2x - 20
f'(x) = 2(3x2 + x - 10)
f'(x) = 2(x + 2)(3x - 5)
To find critical numbers, equate f'(x) to zero and solve for x.
f'(x) = 0
2(x + 2)(3x - 5) = 0
(x + 2)(3x - 5) = 0
x + 2 = 0 or 3x - 5 = 0
x = -2 or x = ⁵⁄₃
Critical numbers are -2 and ⁵⁄₃.
The values -2 and ⁵⁄₃ divide the real line (the domain of f(x)) into intervals (-∞, -2), (-2, ⁵⁄₃) and (⁵⁄₃, ∞).

Notes :
(i) If the critical numbers are not included in the intervals, then the intervals of increasing (decreasing) becomes strictly increasing (strictly decreasing).
(ii) The intervals of increasing/decreasing can be obtained by taking and checking a sample point in the sub-interval.
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
©All rights reserved. onlinemath4all.com
Recent Articles
-
SAT Math Practice
Dec 05, 25 04:04 AM
SAT Math Practice - Different Topics - Concept - Formulas - Example problems with step by step explanation -
10 Hard SAT Math Questions (Part - 37)
Dec 03, 25 07:02 AM
10 Hard SAT Math Questions (Part - 37) -
Factorial Problems and Solutions
Dec 02, 25 09:27 AM
Factorial Problems and Solutions

