DECIMALS

We have learnt about very big numbers (a number with more number of digits) and fractions which is less than 1. We often use fractions like 1/4, 1/2, 3/4.

By addition or subtraction of fractions, we got fractions like 3/8, 5/8, 7/16.

Very numbers also can be written as fractions. Why can't we use fractions to represent all small numbers ?

It is because of the difficulties in using fractions. 

(2/3) + (3/4)  =  ?

We have to convert them into like fractions by finding equivalent fractions and then add.

It is easy, if all the fractions are in the form of 1/10, 1/100, 1/1000...

(15/100) + (235/1000) can be easily added as

(150/1000) + (235/1000)  =  385/1000

It was easy to use multiples of 10 in measurements. It will be easy, if small numbers can be written as fractions with multiples of ten as denominators.  

One Tenths (1/10)

Look at the figure given below. 

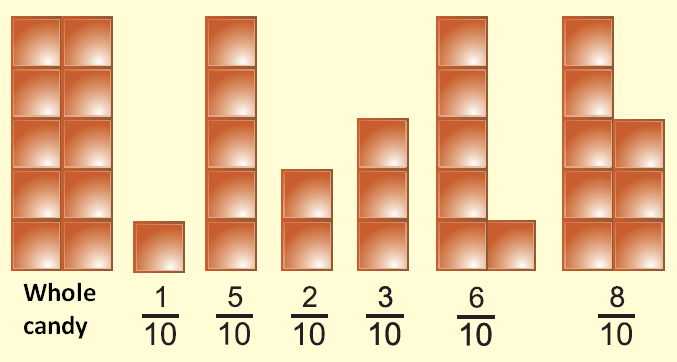
David has 6 candy bars, each connected with 10 connected pieces. 

He gave some pieces to his friends and he finds that 

1 piece out of 10 from the first bar

5 pieces out of 10 from the second bar

2 piece out of 10 from the third bar

3 pieces out of 10 from the fourth bar

6 piece out of 10 from the fifth bar

8 pieces out of 10 from the sixth bar

We can write them as 

1/10, 5/10, 2/10, 3/10, 6/10, 8/10 in fractions. 

This can be written as 0.1, 0.5, 0.2, 0.3, 0.6, 0.8 in decimal numbers. 

0.1 is read as zero point one. The point between between the numbers is called decimal point. 

Decimal Numbers - Definition

A number in which we have "point" is called as decimal number. 

A decimal number has two parts namely an integral part and a decimal part. 

Examples :

1)  Let us consider the decimal number 0.6

0.6 can be written as 0 + 0.6 

Here, integral part  =  0 and decimal part  =  6

2)  Let us consider the decimal number 7.2

7.2 can be written as 7 + 0.2 

Here, integral part  =  7 and decimal part  =  2

In a decimal number the digits to the left of the decimal point is the integral part. 

The digits to the right of the decimal point is the decimal part. 

The value of all the decimal parts is less than 1. 

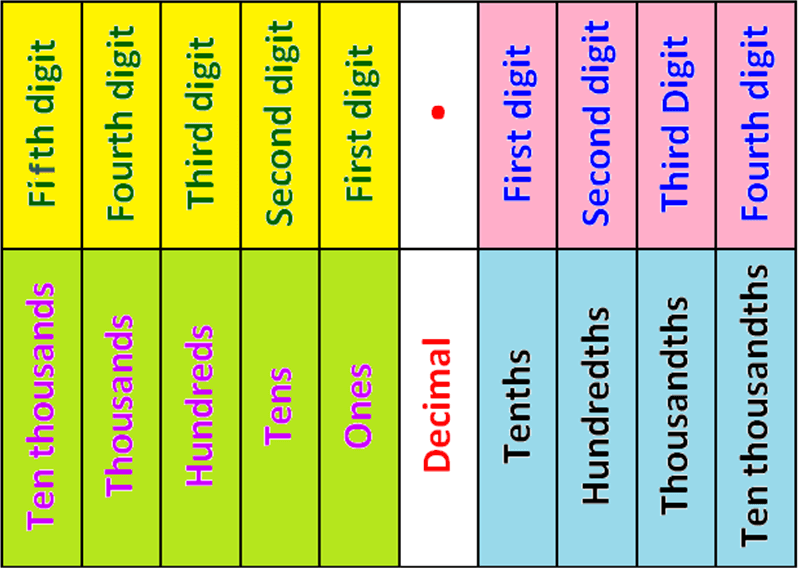
Decimal Place Value

Decimal place value is nothing but the one which explains the position of each digit which comes after the decimal point.

Decimal Place Value Chart

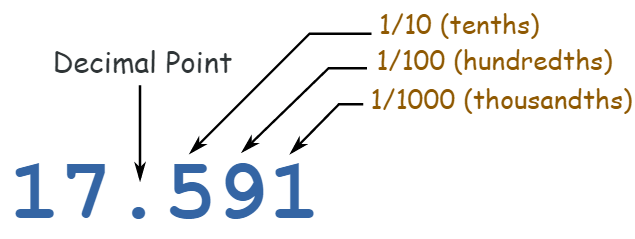
Decimal Place Value - Example

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.