DECIMAL WORD PROBLEMS

Problem 1 :

A chemist mixed 6.35 grams of one compound with 2.45 grams of another compound. How many grams were there in the mixture?

Solution :

Amount of compound in the mixture is 

= 6.35 + 2.45

= 8.8 grams

Problem 2 :

If the cost of a pencil is $1.25, find the cost of 10 pencils. 

Solution :

To find the cost of 10 pencils, we have to multiply the cost of one pencil by 10.

= 100 ⋅ 1.25

Since 1.25 is multiplied by 10, the decimal point has to be moved to the right by one digit. 

= 12.5

The cost of 10 pencils is $12.50.

Problem 3 :

Mr. James walks a distance of 365.7 ft. of distance in 100 minutes. Find the distance he walks in one minute.

Solution :

To find the distance that Mr. James walks in one minute, we have to divide the distance walked in 10 minutes by 10.

= 365.7/100

Since 365.7 is divided by 100, the decimal point has to be moved to the left by two digits.  

= 3.657

James walks a distance of 3.657 ft. in one minute.

Problem 4 :

If the cost of a pen is $10.50, a book is $25.75 and a bag is $45.50, then find the total cost of 2 books, 3 pens and 1 bag. 

Solution :

Total cost of 2 books, 3 pens and 1 bag is 

= 2(25.75) + 3(10.50) + 1(45.50)

= 51.50 + 31.50 + 45.50

= $128.50

Problem 5 :

John wants to buy a bicycle that cost $ 450.75. He has saved $ 125.35. How much more money must John save in order to have enough money to buy the bicycle ?

Solution :

Amount of money that John still has to save is

= 450.75 - 125.35

= $325.40

Problem 6 :

Jennifer bought 6.5 kg of sugar. she used 3750 grams. How many kilograms of sugar were left ?

Solution :

3750 grams = 3750/1000 kg

3750 grams = 3.75 grams

Amount of sugar left (in kilograms) is 

= 6.5 - 3.75

= 2.75 kg

Problem 7 :

The inner radius of a pipe is 12.625 mm and the outer radius is 18.025 mm. Find the thickness of the pipe.

Solution :

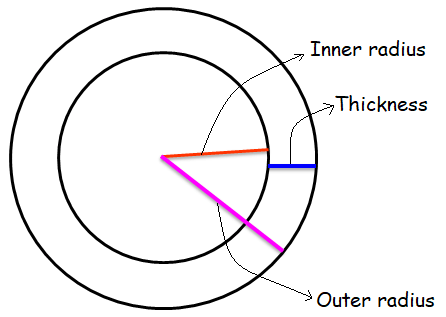
Thickness of the pipe is 

= Outer radius - Inner radius

= 18.025 - 12.625

= 5.40 mm

Problem 8 :

A copy of English book weighs 0.45 kg. What is the weight of 20 copies ? 

Solution :

Weight of 20 copies of English book is 

= 20 ⋅ 0.45

= 9 kg

Problem 9 :

Find the weight of 25.5 meters of copper wire in kilograms, if one meter weighs 10 grams.

Solution :

Weight of 25.5 meters of copper wire is 

= 25.5 ⋅ 10

= 255 grams

= 255/1000 kilograms

= 0.255 kilograms

Problem 10 :

Robert paid $140 for 2.8 kg of cooking oil. How much did 1 kg of the cooking oil cost ?

Solution :

The cost of 1 kg of cooking oil is 

= 140/2.8

= $50

Problem 11 :

If $20.70 is earned in 6 hours, how much money will be earned in 5 hours ?

Solution :

Amount of money earned in 1 hour is

= 20.70/6

= 3.45

Amount of money earned in 5 hours is

= 5 ⋅ 3.45

 = $17.25

Problem 12 :

A pipe is 76.8 meters long. What will be the greatest number of pieces of pipe each 8 meters long that can be cut from this pipe ?

Solution :

Greatest number of pieces can be cut from the pipe is 

= 76.8/8

= 9.6

So, 9 pieces of pipe each 8 meters long can be cut from the pipe of length 76.8 meters.

Problem 13 :

When the decimal number 2.78A is multiplied by 100, the answer is 278.5 Find the value of A.

Solution :

When the decimal number 2.78A is multiplied by 100, the decimal point has to be moved to the right by two digits.

2.78A x 100 = 278.A ----(1)

It is given that dividing the decimal number 2.78A by 100 results 278.5.

2.78A x 100 = 278.5 ----(2)

Comparing (1) and (2),

278.A = 278.5

If two decimal numbers are equal, then the digits at tenths places must be equal.

Therefore,

A = 5

Problem 14 :

If ten-thousandth of a number is 0.0005, find the number.

Solution :

It is given that ten-thousandth of the decimal number is 0.0005.

Let k be the number.

Then, from the given information, we get

(1/10000) x k = 0.0005

Multiply both sides by 10000.

k = 0.0005 x 10000

Since 0.0005 is multiplied by 10000, the decimal point has to be moved to the right by four digits.

k = 5

Therefore, the number is 5.

Problem 15 :

Evaluate the following expression with the conditions given below.

a.b + b.a

Conditions :

(i) Both a and b are positive integers.

(ii) Both a and b are prime numbers and a is an even number.

Solution :

From the given conditions,

a = 2 and b = 3

a.b + b.a :

= 2.3 + 3.2

= 5.5

Click here to get detailed answers for the above questions.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.