DECIMAL PLACE VALUE

Place value is a positional system of notation in which the position of a number with respect to a point determines its value.

In the decimal (base ten) system, the value of the digits is based on the number ten. Each position in a decimal number has a value that is a power of 10.

A decimal point separates the positive exponents of 10 on the left and the negative exponents of 10 on the right.   

That is, we have the following positive exponents of 10 on the left side of the decimal point. 

10⁰  =  1, 10¹  =  10, 10²  =  100, 10³  =  1,000

We have the following negative exponents of 10 on the right side of the decimal point. 

10^-1  =  1/10, 10^-2  =  1/100, 10^-3  =  1/1000

Decimal Place Value Chart

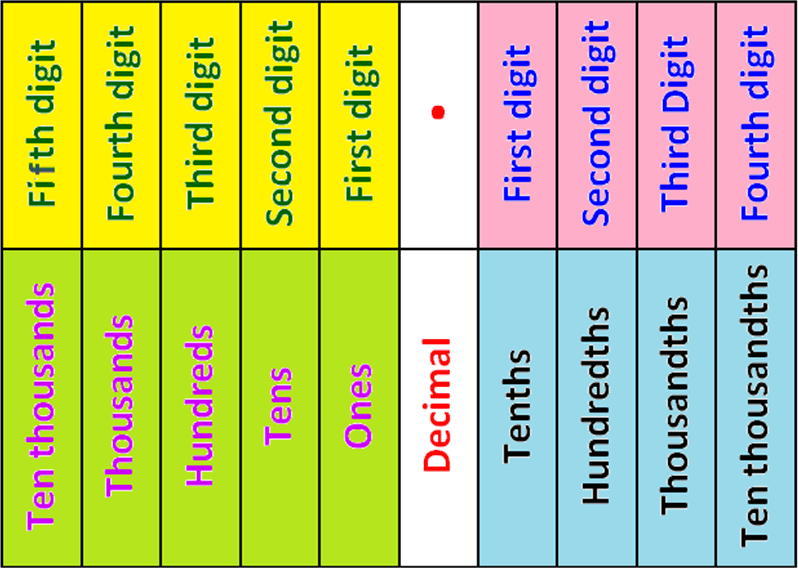
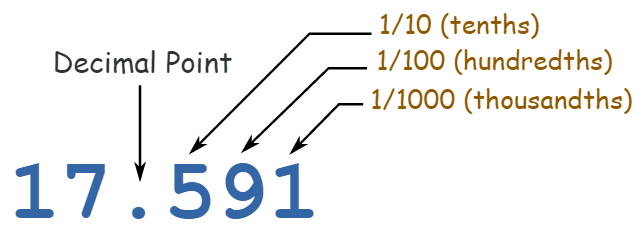
To have better understanding on the above chart, let us look at an example.

Solved Questions

Question 1 : 

In 0.5276, which digit is in the tenths place?

Answer :

Tenths place is nothing but the position of first digit after the decimal point. 

In 0.5276, the first digit after the decimal point is 5. 

So, the digit in the tenths place is 5.

Question 2 : 

In 1.2347, which digit is in the hundredths place?

Answer :

Hundredths place is nothing but the position of second digit after the decimal point. 

In 1.2347, the second digit after the decimal point is 3. 

So, the digit in the hundredths place is 3.

Question 3 : 

In 5678.92, which digit is in the hundreds place?

Answer :

Hundreds place is nothing but the position of second digit before the decimal point. 

In 5678.92, the second digit before the decimal point is 7.

So, the digit in the hundreds place is 7.

Question 4 : 

In 207.159, in which place is the 9 ? 

Answer :

In 207.159, "9" is the third digit after the decimal point. 

According to the decimal place value chart, 9 is at thousandths place.  

So, 9 is at thousandths place. 

Question 5 : 

In 58702.19 in which place is the 7 ? 

Answer :

In 58702.19, "7" is the third digit before the decimal point. 

According to the decimal place value chart, 7 is at hundreds place. 

So, 7 is at hundreds place.

Question 6 :

In 13256.02, which digit is in the ten thousands place?

Answer :

Ten thousands place is nothing but the position of fifth digit before the decimal point.

In 13256.02, the fifth digit after the decimal point is 1.

So, the digit in the thousands place is 1.

Question 7 : 

Write the given verbal phrase as a decimal number.

"sixty-five, five-tenths and seven-hundredths"

Answer :

From the given verbal phrase, we can have the numbers and their positions as given below.

6 - tens

5 - ones

5 - tenths

7 - hundredths

So, we have

"sixty-five, five-tenths and seven-hundredths"  =  65.57

Question 8 : 

Write the given verbal phrase as a decimal number.

"seventy-four and eight-thousandths"

Answer :

7 - tens 

4 - ones

0 - tenths

0 - hundredths

8 - thousandths

So, we have

"seventy-four and eight-thousandths"  =  74.008

Question 9 : 

Multiply 0.36 and 0.24 and round the answer to the nearest hundredths.

Answer :

0.36 x 0.24  =  0.0864

Whenever we want to round the number to the nearest hundredths, first we have to look at the digit at thousandths place. If it is greater than or equal to 5, we have to add 1 to the digit at hundredths place. 

Here, the digit at the thousandths place is 6 which is greater than 5. 

So we have to add 1 to the digit at the hundredths place. 

So, we have

0.0864  ≈  0.09

Question 10 : 

Divide 5 by 1.2 and round the answer to the nearest thousandths.

Answer :

5/1.2  =  50/12

5/1.2  =  4.166666...........

Whenever we want to round the number to the nearest thousandths, first we have to look at the digit at ten thousandths place. If it is greater than or equal to 5, we have to add 1 to the digit at thousandths place. 

Here, the digit at the ten thousandths place is 6 which is greater than 5. 

So we have to add 1 to the digit at the thousandths place. 

So, we have

4.16666.......  ≈  4.167

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.