CUSTOMARY UNITS OF TIME

Customary units of time is a system of measurements commonly used for time in the united states.

For measuring time, the U.S. customary system uses the second, minute, hour, day, week, month and year which are the only seven customary time measurements in everyday use.

The relationship among the measurements second, minute, hour, day, week, month and year are given below.

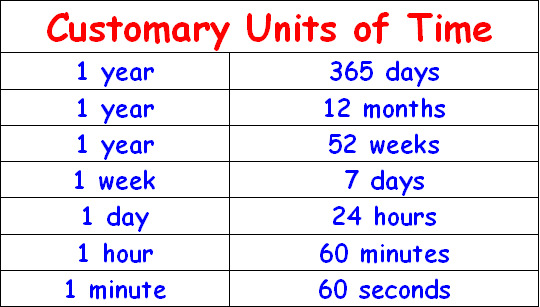
Conversions

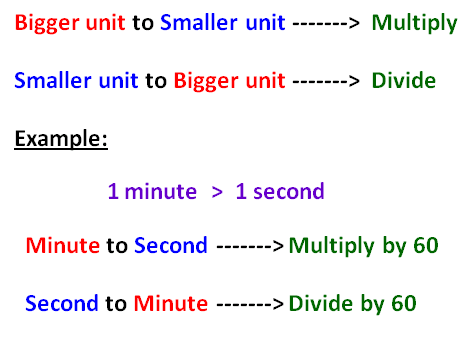
Solved Problems

Problem 1 :

Convert 2 minutes into seconds. 

Solution :

Here, we convert bigger unit into smaller unit. So we have to multiply.

2 minutes  =  2 ⋅ 60 seconds 

=  120 seconds

So, 2 minutes is equal to 60 seconds.

Problem 2 :

Convert 3.5 hours into minutes  . 

Solution :

Here, we convert bigger unit into smaller unit. So we have to multiply.

3.5 hours  =  3.5 x 60 minutes

=  210 minutes

So, 3.5 hours is equal to 210 minutes.

Problem 3 :

Convert 3 days into minutes. 

Solution :

Here, we convert bigger unit into smaller unit unit. So we have to multiply.

3 days  =  3 x 24 hours 

=  72 hours

=  72 x 60 minutes

=  4320 minutes

So, 3 days is equal to 4320 minutes.

Problem 4 :

Convert 480 seconds into minutes. 

Solution :

Here, we convert smaller unit into bigger unit. So we have to divide.

480 seconds  =  480/60 minutes 

=  6 minutes

So, 480 seconds is equal to 6 minutes. 

Problem 5 :

Convert 112 days into weeks. 

Solution :

Here, we convert smaller unit into bigger unit. So we have to divide.

112 days  =  112/7 weeks 

=  16 weeks

So, 112 days is equal to 16 weeks.

Problem 6 : 

David prepares 24 pounds of metal in 1 hour 36 minutes. At the same rate, How many ounces of metal will he prepare in one minute ? 

Solution :

1 hour 36 minutes  =  60 min + 36 min  =  96 minutes

1 pound  =  16 ounces

24 pounds  =  24 ⋅ 16 ounces  =  384 ounces

1 hour 36 min -----> 24 pounds

96 minutes -----> 384 pounds

So, no. of pounds prepared in 96 minutes is 384 ounces.

No. of ounces prepared in in one minute is

=  384/96  

=  4

So, 4 ounces of metal is prepared in one minute.

Problem 7 : 

Mark used 15840 ounces of metal to make an alloy in 45 minutes. Find the amount metal used in one minute (in ounces).

Solution :

No. of ounces used in 45 minutes  =  15840

=  15840/45

=  352

So, 352 ounces of metal used in 1 minute. 

Problem 8 : 

Mrs. Moore took 4 hours 30 minutes to complete a work. How many seconds will Mrs. Moore take to complete the same work ?

Solution :

4 hours 30 minutes  =  4 ⋅ 60 min + 30 min

=  240 min + 30 min

=  270 minutes

=  270 ⋅ 60 seconds

=  16200 seconds

So, Mrs. Moore will take 16200 seconds to complete the same work. 

Problem 9 : 

Tommy takes 10 minutes time for each pizza he makes. How many seconds will he take to make 4 pizzas ?

Solution :

1 pizza -----> 10 minutes

4 pizzas -----> 4 ⋅ 10 minutes

4 pizzas ------> 40 minutes

4 pizzas ------> 40 ⋅ 60 seconds

4 pizzas ------> 2400 seconds

So, Tommy will take 2400 seconds to make 4 pizzas. 

Problem 10 : 

A piece of work can be done by Mr. David in 9 days working 10 hours per day. How many hours will be taken by Mr. David to complete another work which is 4 times the first one ?

Solution :

Time needed to complete the given work is

=  9 ⋅ 10 hours

=  90 hours

Time needed to complete another work which is 4 times the first first work is

=  4 ⋅ 90 hours

=  360 hours

So, the required time is 360 hours. 

Problem 11 : 

Jose needs 6 hours to complete a work. But Jacob need 3/4 of time taken by Jose to complete the same work. In how many minutes will Jose complete the work ? 

Solution :

Time required for Jose :

=  6 hours

Time required for Jacob :

=  3/4 of time taken Jose

=  3/4 ⋅ 6 hours

=  3/4 ⋅ 6 ⋅ 60 minutes

=  270 minutes

So, Jacob needs 270 minutes to complete the work. 

Problem 12 : 

Robert has been given 2 hours to complete a work. If the time is reduced by 25%, in how many minutes will he complete the same work ? 

Solution :

Time taken by Robert to complete the work  =  2 hours

If the time is reduced by 25%,  

Time taken by Robert to complete the work is

=  75% of 2 hours

=  0.75 ⋅ 2 hours

=  0.75 ⋅ 2 ⋅ 60 minutes

=  90 minutes

So, Robert will take 90 minutes to complete the work. 

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.