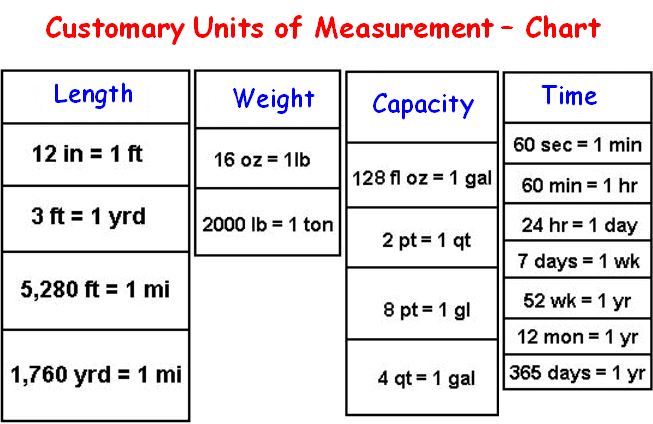
CUSTOMARY UNITS OF MEASUREMENT CHART

Customary units of measurement chart is the one which gives a system of measurements commonly used for length, weight, capacity and time in the united states. 

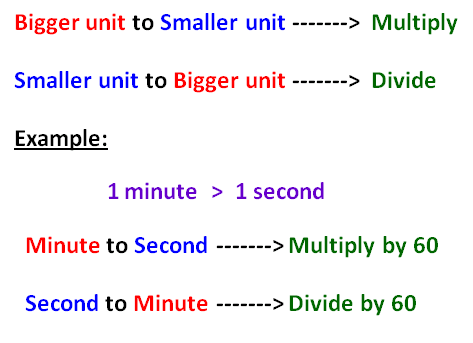
Conversions

Solved Problems

Problem 1 :

Convert 2 feet into inches.

Solution :

Here, we convert bigger unit into smaller unit. So we have to multiply.

2 feet  =  2 ⋅ 12 inches

2 feet  =  24 inches

So, 2 feet is equal to 24 inches.

Problem 2 :

Convert 3.5 yards into inches.

Solution :

Here, we convert bigger unit into smaller unit. So we have to multiply.

3.5 yards  =  3.5 ⋅ 36 inches

3.5 yards  =  126 inches

So, 3.5 yards is equal to 126 inches.

Problem 3 :

Convert 30 inches into feet. 

Solution :

Here, we convert smaller unit into bigger unit. So we have to divide.

30 inches  =  30/12 feet 

30 inches  =  2.5 feet

So, 30 inches is equal to 2.5 feet.

Problem 4 :

Convert 5280 yards into miles. 

Solution :

Here, we convert smaller unit into bigger unit. So we have to divide.

5280 yards  =  5280/1760 miles 

5280 yards  =  3 miles

So, 5280 yards is equal to 3 miles.

Problem 5 :

Convert 24 feet into yards 

Solution :

Here, we convert smaller unit into bigger unit. So we have to divide.

24 feet  =  24/3 yards 

24 feet  =  8 yards 

So, 24 feet is equal to 8 yards

Problem 6 :

Convert 2 pounds into ounces. 

Solution :

Here, we convert bigger unit into smaller unit. So we have to multiply.

2 pounds  =  2 ⋅ 16 ounces 

2 pounds  =  32 ounces

So, 2 pounds is equal to 32 ounces.

Problem 7 :

Convert 3.5 tons into pounds  . 

Solution :

Here, we convert bigger unit into smaller unit. So we have to multiply.

3.5 tons  =  3.5 ⋅ 2000 pounds

3.5 tons  =  7000 pounds

So, 3.5 tons is equal to 7000 pounds.

Problem 8 :

Convert 0.5 tons into ounces. 

Solution :

Here, we convert bigger unit into smaller unit. So we have to multiply.

0.5 tons  =  0.5 ⋅ 2000 pounds 

0.5 tons  =  1000 pounds

0.5 tons  =  1000 ⋅ 16 ounces

0.5 tons  =  16000 ounces

So, 0.5 tons is equal to 16000 ounces.

Problem 9 :

Convert 48 ounces into pounds. 

Solution :

Here, we convert smaller unit into bigger unit. So we have to divide.

48 ounces  =  48/16 pounds 

48 ounces  =  3 pounds

So, 48 ounces is equal to 3 pounds. 

Problem 10 :

Convert 5000 pounds into tons 

Solution :

Here, we convert smaller unit into bigger unit. So we have to divide.

5000 pounds  =  5000/2000 tons 

5000 pounds  =  2.5 tons

So, 5000 pounds is equal to 2.5 tons.

Problem 11 :

Convert 2 pints into cups. 

Solution :

Here, we convert bigger unit into smaller unit. So we have to multiply.

2 pints  =  2 ⋅ 2 cups 

2 pints  =  4 cups

So, 2 pints is equal to 4 cups.

Problem 12 :

Convert 3.5 quarts into cups  . 

Solution :

Here, we convert bigger unit into smaller unit. So we have to multiply.

3.5 quarts  =  3.5 ⋅ 4 cups

3.5 quarts  =  14 cups

So, 3.5 quarts is equal to 14 cups.

Problem 13 :

Convert 32 cups into quarts. 

Solution :

Here, we convert smaller unit into bigger unit. So we have to divide.

32 cups  =  32/4 quarts 

32 cups  =  8 quarts

So, 32 cups is equal to 8 quarts.

Problem 14 :

Convert 256 cups into gallons. 

Solution :

Here, we convert smaller unit into bigger unit. So we have to divide.

256 cups  =  256/16 gallons 

256 cups  =  16 gallons

So, 256 cups is equal to 16 gallons.

Problem 15 :

Convert 24 quarts into gallons 

Solution :

Here, we convert smaller unit into bigger unit. So we have to divide.

24 quarts  =  24/4 gallons 

24 quarts  =  6 gallons 

So, 24 quarts is equal to 6 gallons.

Problem 16 :

Convert 2 minutes into seconds. 

Solution :

Here, we convert bigger unit into smaller unit. So we have to multiply.

2 minutes  =  2 ⋅ 60 seconds 

2 minutes  =  120 seconds

So, 2 minutes is equal to 60 seconds.

Problem 17 :

Convert 3.5 hours into minutes  . 

Solution :

Here, we convert bigger unit into smaller unit. So we have to multiply.

3.5 hours  =  3.5 ⋅ 60 minutes

3.5 hours  =  210 minutes

So, 3.5 hours is equal to 210 minutes.

Problem 18 :

Convert 3 days into minutes. 

Solution :

Here, we convert bigger unit into smaller unit unit. So we have to multiply.

3 days  =  3 ⋅ 24 hours 

3 days  =  72 hours

3 days  =  72 ⋅ 60 minutes

3 days  =  4320 minutes

So, 3 days is equal to 4320 minutes.

Problem 19 :

Convert 480 seconds into minutes. 

Solution :

Here, we convert smaller unit into bigger unit. So we have to divide.

480 seconds  =  480/60 minutes 

480 seconds  =  8 minutes

So, 480 seconds is equal to 8 minutes. 

Problem 20 :

Convert 112 days into weeks. 

Solution :

Here, we convert smaller unit into bigger unit. So we have to divide.

112 days  =  112/7 weeks 

112 days  =  16 weeks

So, 112 days is equal to 16 weeks.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.