CUSTOMARY UNITS OF LENGTH

Customary units of length is a system of measurements commonly used for length in the united states. 

Word problems given in this section will be much useful for the students who would like to practice problems on customary units of length like inch, foot, yard and mile

For measuring length, the U.S. customary system uses the which are the only four customary length measurements in everyday use. 

The relationship among the measurements inch, foot, yard  and mile  are given below.

12 inches  =  1 foot

3 feet  =  1 yard

5280 feet  =  1 mile

1760 yards  =  1 mile

Customary Units of Length - Conversion

Customary Units of Length - Practice Problems

Problem 1 :

Convert 2 feet into inches. 

Solution : 

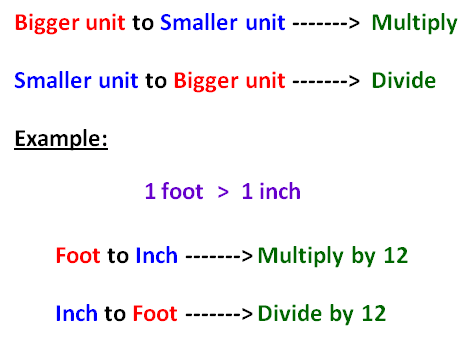
Here, we convert bigger unit into smaller unit. So we have to multiply.

2 feet  =  2 ⋅ 12 inches 

2 feet  =  24 inches

Hence, 2 feet is equal to 24 inches.

Problem 2 :

Convert 3.5 yards into inches. 

Solution : 

Here, we convert bigger unit into smaller unit. So we have to multiply.

3.5 yards  =  3.5 ⋅ 36 inches

3.5 yards  =  126 inches

Hence, 3.5 yards is equal to 126 inches.

Problem 3 :

Convert 30 inches into feet. 

Solution : 

Here, we convert smaller unit into bigger unit. So we have to divide.

30 inches  =  30 / 12 feet 

30 inches  =  2.5 feet

Hence, 30 inches is equal to 2.5 feet.

Problem 4 :

Convert 5280 yards into miles. 

Solution : 

Here, we convert smaller unit into bigger unit. So we have to divide.

5280 yards  =  5280 / 1760 miles 

5280 yards  =  3 miles

Hence, 5280 yards is equal to 3 miles.

Problem 5 :

Convert 24 feet into yards 

Solution : 

Here, we convert smaller unit into bigger unit. So we have to divide.

24 feet  =  24 / 3 yards 

24 feet  =  8 yards 

Hence, 24 feet is equal to 8 yards

Customary Units of Length - Word Problems

Problem 1 : 

David travels 60 miles in two hours. How many yards of distance will he cover in one minute ? 

Solution : 

We know that, 

1 hour  =  60 minutes

1 mile  =  1760 yards

Given : Distance covered in 2 hours is 60 miles. 

Then, we have

Distance covered in 1 hour  =  30 miles

Distance covered in 1 hour  =  30 ⋅ 1760 yards

Distance covered in 60 minutes  =  30 ⋅ 1760 yards

Distance covered in 60 minutes  =  52800 yards

Distance covered in 1 minute  =  52800 / 60 yards 

Distance covered in 1 minute  =  880 yards

So, David will cover 880 yards of distance in 1 minute.

Problem 2 : 

Mark jogged 15840 feet in 45 minutes. Find the speed of Mark in feet per minute. 

Solution : 

Speed  =  Distance / Time

Speed  =  15840 / 45

Speed  =  352 feet per minute

So, the speed of Mark is 352 feet per minute. 

Problem 3 : 

Use a fraction to find the length in feet of a shoe that is 9 inches long. 

Solution : 

Here, we convert smaller unit (inches) into larger unit (foot).

So we have to divide.

Because, 1 foot  is  equal 12 inches, we have to use the fraction 1/12.

9 inches  =  9 ⋅ 1/12 ft

9 inches  =  3/4 ft

So, the length of the shoe is 3/4 ft. 

Problem 4 : 

Kevin has a new television that is 24 inches tall. If Kevin sets the television on a 3-foot-tall stand, how far from the floor will the top of the television be (in inches) ?

Solution : 

Given : Height of the television is 24 inches. 

Height of the stand is

=  3 feet

=  3 ⋅ 12

=  36 inches

Distance from the floor to the top of the television is 

=  Height of the stand + Height of the television

=  36 + 24 

=  60 inches

So, the top of the television is 60 inches far from the floor. 

Problem 5 : 

Becky and Keith each ran for exactly 20 minutes on a treadmill. Keith’s treadmill said he had run 10,000 feet. Becky’s treadmill said she had run 2 miles. Who ran farther, and how much farther?

Solution : 

Both Becky and Keith took the same amount of time. That is 20 minutes.

Distance covered by Becky and Keith are given in different units. (Miles and Feet)

We have to make the units to be same. 

Let us convert miles in to feet. 

So,

2 miles  =  2 ⋅ 5280 feet

2 miles  =  10560 feet 

Therefore,

Distance covered by Becky  =  10560 feet -----(1) 

Distance covered by Keith  =  10000 feet -----(2)

Difference between (1) and (2) is 

=  10560 - 10000

=  560 feet

So, Becky ran farther by 560 feet. 

Apart from the stuff given in this section, if you need any other stuff in math, please use our google custom search here. 

If you have any feedback about our math content, please mail us : 

v4formath@gmail.com

We always appreciate your feedback. 

You can also visit the following web pages on different stuff in math. 

WORD PROBLEMS

HCF and LCM  word problems

Word problems on simple equations 

Word problems on linear equations 

Word problems on quadratic equations

Algebra word problems

Word problems on trains

Area and perimeter word problems

Word problems on direct variation and inverse variation 

Word problems on unit price

Word problems on unit rate 

Word problems on comparing rates

Converting customary units word problems 

Converting metric units word problems

Word problems on simple interest

Word problems on compound interest

Word problems on types of angles 

Complementary and supplementary angles word problems

Double facts word problems

Trigonometry word problems

Percentage word problems 

Profit and loss word problems 

Markup and markdown word problems 

Decimal word problems

Word problems on fractions

Word problems on mixed fractrions

One step equation word problems

Linear inequalities word problems

Ratio and proportion word problems

Time and work word problems

Word problems on sets and venn diagrams

Word problems on ages

Pythagorean theorem word problems

Percent of a number word problems

Word problems on constant speed

Word problems on average speed 

Word problems on sum of the angles of a triangle is 180 degree

OTHER TOPICS 

Profit and loss shortcuts

Percentage shortcuts

Times table shortcuts

Time, speed and distance shortcuts

Ratio and proportion shortcuts

Domain and range of rational functions

Domain and range of rational functions with holes

Graphing rational functions

Graphing rational functions with holes

Converting repeating decimals in to fractions

Decimal representation of rational numbers

Finding square root using long division

L.C.M method to solve time and work problems

Translating the word problems in to algebraic expressions

Remainder when 2 power 256 is divided by 17

Remainder when 17 power 23 is divided by 16

Sum of all three digit numbers divisible by 6

Sum of all three digit numbers divisible by 7

Sum of all three digit numbers divisible by 8

Sum of all three digit numbers formed using 1, 3, 4

Sum of all three four digit numbers formed with non zero digits

Sum of all three four digit numbers formed using 0, 1, 2, 3

Sum of all three four digit numbers formed using 1, 2, 5, 6