CURVED SURFACE AREA OF CYLINDER

Curved surface area of cylinder is the measurement of outer area,  where the extension of top and bottom portion wont be included. 

Curved surface area of cylinder

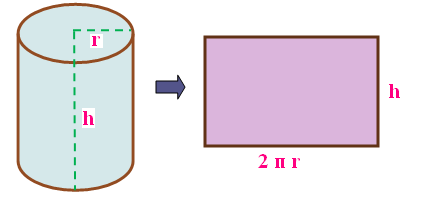
If a rectangle revolves about one side and completes one full rotation, the solid thus formed is called a right circular cylinder. The above picture shows that how rectangle forms a right circular cylinder. In other words curved surface area is simply said as CSA 

CSA of cylinder = 2 π r h

"r" and "h" stands for radius and height of cylinder.

Curved surface area of hollow cylinder

A hollow cylinder is a three dimensional solid bounded by two parallel cylindrical surfaces and by two parallel circular bases cut out from two parallel planes by these two cylindrical surfaces.

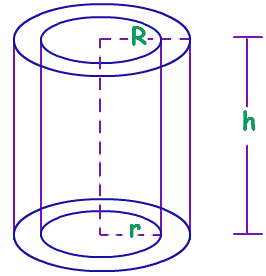
CSA of hollow cylinder = 2πh(R+r)

R  =  external radius, r = internal radius and h  =  height

Example problems of curved surface area of cylinder 

Example 1 :

A solid right circular cylinder has radius of 14 cm and height of 8 cm. Find its CSA.

Solution :

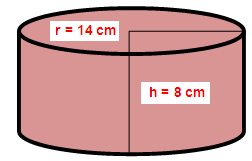
Radius of the cylinder (r)  =  14 cm

Height of the cylinder (h)  =  8 cm

Curved surface area of cylinder  =  2Πrh

=  2⋅ (22/7) ⋅ 14 ⋅  8

=  704 sq.cm

Curved surface area of cylinder  =  704 sq.cm

So, curved surface area of cylinder is 704 sq.cm

Example 2 :

Curved surface area and circumference at the base of a solid right circular cylinder are 4400 sq.cm and 110 cm respectively. Find its height and diameter.

Solution :

CSA of cylinder  =  4400 sq.cm

Circumference of the base  =  110 cm

2Πr  =  110 ==> 2 ⋅ (22/7) ⋅ r  =  110

r  =  110 ⋅ (1/2) ⋅ (7/22)

r  =  17.5 cm

diameter  =  2r  =  2(17.5)

diameter  =  35 cm 

2 Π r h   =   4400

110 ⋅ h  =  4400

h  =  4400/110

h  =  40 cm 

Height  =  40 cm

Diameter of the cylinder  =  35 cm

So, height and diameter of cylinder is 40 cm and 35 cm respectively.

Example 3 :

A mansion has 12 right cylindrical pillars each having radius 50 cm and height 3.5 m. Find the cost to paint the curved surface of pillars at $ 20 per square meter.

Solution :

The pillars of the mansion are in the shape of cylinder 

Radius = 50 cm ==>  0.5 m

Height = 3.5 m

CSA of one pillar   =  2 ⋅ (22/7) ⋅ 0.5 ⋅ 3.5

=   2 ⋅ 22 ⋅ 0.5 ⋅ 0.5 ==> 11 m²

CSA of 12 pillars  =  12 ⋅ 11 

=  132 m²

Cost to paint per m²  =  $ 20

Total cost  =  20 ⋅ 132

=  $ 2640   

Hence, total cost of painting 12 pillars is $ 2640

Example 4 :

The total surface area of a solid right circular cylinder are 231 cm². Its curved surface area is two thirds of the total surface area. Find the curved surface area if cylinder.

Solution :

Curved surface area = (2/3) ⋅ Total surface area

                      2 Π r h  =  (2/3) ⋅ 231

                      2 Π r h  =  2 ⋅ 77

                      2 Π r h  =  154

Hence, curved surface area of cylinder is 154 cm²

Example 5 :

The total surface area of a solid right circular cylinder is 1540 cm². If the height is four times the radius of the base, then find the CSA of cylinder.

Solution :

Total surface area of cylinder  =  1540 cm²

CSA of cylinder + top area + bottom area = 1540 cm²

2 Π r (h + r)  =  1540

h  =  4 ⋅ radius of the base 

h  =  4 r

2 Π r (4r+r)  =  1540

2 Π r (5r)  =  1540  

 2 ⋅ (22/7) ⋅ 5 r²  =  1540

  =  1540 ⋅ (1/2) ⋅  (7/22) ⋅ (1/5)

  =  (1540 ⋅ 7)/(2 ⋅ 22 ⋅ 5)

  =  (1540 ⋅ 7 )/(2 ⋅ 22 ⋅ 5)

 r²  =  49

 r  =   √(7⋅7)

 r  =  7 cm

Curved surface area of cylinder :

=  1540 - 2 ⋅ (22/7) ⋅ 7 ⋅ 7

=  1540 - 308

=  1232 cm²

Hence, CSA of cylinder  =  1232 cm².

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.