CURVED SURFACE AREA AND TOTAL SURFACE AREA OF CYLINDER EXAMPLES

Formula for Curved Surface Area and Total Surface Area of Cylinder

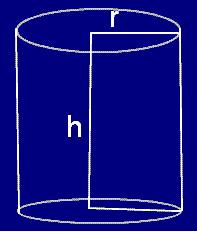	Curved surface area  =  2Πrh Total surface area of  =  2Πr(h + r)
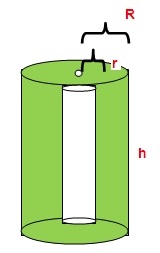	Curved surface area    =  2Π(R + r)h Total surface area    =  2Π(R + r)(R - r + h)

Example 1 :

The radius and height of a cylinder are in the ratio 5:7 and its curved surface area is 5500 sq.cm. Find its radius and height.

Solution :

Radius of cylinder (r)  =  5x

Height of cylinder (h)  =  7x

Curved surface area of cylinder  =  5500 sq.cm

 2Πrh  =  5500

2⋅(22/7) ⋅ 5x ⋅ 7x  =  5500

x²  =  5500 (7/22) ⋅ (1/2) ⋅ (1/35)

x²  =  25

x  =  5

Radius  =  5(5)  =  25 cm

Height  =  7(5)  =  35 cm

Example 2 :

A solid iron cylinder has total surface area of 1848 sq.m. Its curved surface area is five – sixth of its total surface area. Find the radius and height of the iron cylinder.

Solution :

Total surface area of cylinder  =  1848 sq.cm

curved surface area  =  (5/6) of 1848

  =  (5/6) 1848

 2Πrh  =  1540----(1)

 2Πr(h + r)  =  1848

 2Πrh + 2Πr²  =  1848

1540 + 2Πr²  =  1848

2Πr²  =  1848 - 1540

2(22/7)r²  =  308

r²  = 308 (7/22)(1/2)

r²  =  49

r  =  7 m

By applying the value of r in (1), we get 

 2 ⋅ (22/7) ⋅ 7 h  =  1540

h  =  1540/44

 h  = 35 m

Example 3 :

The external radius and the length of a hollow wooden log are 16 cm and 13 cm respectively. If its thickness is 4 cm then find its T.S.A.

Solution :

External radius (R)  =  16 cm

height of log  =  13 cm

thickness  =  4 cm

thickness =  R - r ==>  4  =  16 - r

Internal radius (r)  =  16 - 4  =  12 cm

Total surface area  =  2Π(R + r) (R - r + h)

  =  2 ⋅ (22/7) (16 + 12) (16 - 12 + 13)

  =  2 ⋅ (22/7) (28) (17)

  =  2992 cm² 

Example 4 :

Find the curved surface area of the cylinder whose circumference of the base is 22 cm and height is 3m:

(a) 44cm² (b) 66 cm² (c) 77cm² (d) 22cm²

Solution :

Circumference of the base = 22 cm

2Πr = 22

2 x (22/7) x r = 22

r = 22 x (7/22) x (1/2)

r = 7/2

r = 3.5 cm

height (h) = 3 m = 300 cm

Curved surface area = 2Πrh

= 2 x (22/7) x 3.5 x 300

= 6600 cm²

Example 5 :

If the lateral surface of a cylinder is 94.2 sq.cm and its height is 5 cm, then find radius of its base.

Solution :

Lateral surface area = 2Πrh

given that h = 5 cm

2 x (22/7) x r x 5 = 94.2 sq.cm

r = 94.2 x (7/22) x (1/2) x (1/5)

= 659.4/(22 x 2 x 5)

= 2.99

r is approximately 3 cm

Example 6 :

The difference between outside and inside surface of a cylindrical metallic pipe 14 cm long is 44 cm². If the sum of the diameters of the inner and outer surface of the cylinder is 9 cm, find the inner and outer radii of the cylinder

Solution :

Let r be the inner radius and R be the outer radius.

2ΠRh - 2Πrh = 44 cm²

2Πh(R - r) = 44

Here h = 14 cm

2Π(1400)(R - r) = 44

R - r = 44 x (1/2) x (7/22) x (1/14)

R - r = 1/2 ----(1)

2R + 2r = 9 cm ----(2)

(1) x 2 + (2) ==> 4R = 1+9

4R = 10

R = 10/4

R = 5/2 ==> 2.5

Applying the value of R in (1), we get

2.5 - r = 0.5

r = 2.5 - 0.5

r = 2

So, the external radius is 2.5 cm and internal radius is 2 cm.

Example 7 :

A right circular cylinder just encloses a sphere of radius 10 cm. Find the surface area of cylinder.

Solution :

Since the cylinder encloses the sphere

diameter of sphere = height of the cylinder = diameter of cylinder

Radius of cylinder (r) = 5 cm

height of cylinder (h) = 10 cm

Surface of cylinder = 2Πrh

= 2 x (22/7) x 5 x 10

= 314.29 cm²

Example 8 :

.In a hot water heating system there is a cylindrical pipe of length 28 m and diameter 5 cm. Find the total radiating surface area in the system.

Solution :

Length of pipe = 28 m (h) ==> 2800 cm

diameter = 5 cm, radius = 5/2 ==> 2.5 cm

Total surface area = 2Πrh

= 2 x (22/7) x 2.5 x 2800

= 44000 cm²

Example 9 :

The cut wedge represents one eight of the cheese.

a) Find the surface area of the cheese before it is cut.

b) Find the surface area of the remaining cheese after the wedge is removed. Did the surface area increase, decrease or remain the same ?

Solution :

a) radius = 3 inches, thickness or height = 1 inch

Surface area of cylinder = 2Πrh

= 2 x (22/7) x 3 x 1

= 44/21

= 2.09 square inches.

b) To find the remaining cheese after the wedge removed, we have to find 7/8 of the surface area.

= 7/8 x 2.09

= 1.828 square inches.

The surface area is decreased after the wedge is removed.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.