CURVED SURFACE AREA AND TOTAL SURFACE AREA OF CONE

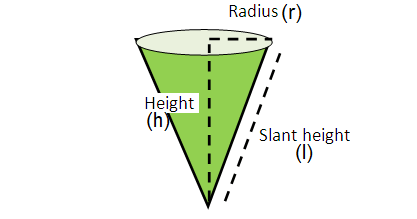
Curved surface area :

 =  πrl

Total surface area of 

=  πr(l + r)

Example 1 :

A right angled triangle PQR where angle Q = 90 degree is rotated about QR and PQ. If QR = 16 cm and PR = 20 cm, compare the curved surface areas of the right circular cones so formed by the triangle.

Solution :

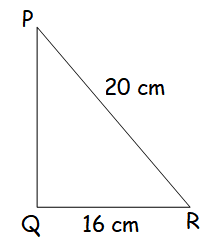
radius of cone  =  16 cm 

Slant height  =  20 cm

If the triangle is rotated about PQ :

Curved surface area =  Πrl

  =  Π ⋅ 16 ⋅ 20

  =  320Π cm²

height  =  √(l² - r²)

 =  √(20² - 16²)

 =  √144

h  =  12

If the triangle is revolved about QR, then radius will be 12 cm

Curved surface area =  Πrl

  =  Π ⋅ 12 ⋅ 20

  =  240Π cm²

So, curved surface area of cone is larger when it is revolved about PQ.

Example 2 :

4 persons live in a conical tent whose slant height is 19 cm. If each person require 22 cm² of the floor area, then find the height of the tent.

Solution :

Slant height of conical tent  =  19 cm

Required area of floor for 1 person  =  22 cm²

Area for 4 persons  =  22(4)  =  88

Πr²  =  88

(22/7) ⋅ r²  =  88

r²  =  88 ⋅ (7/22)

r  =  2√7

height  =  √(l² - r²)

 =  √(19² - (2√7)²

 =  √[361 - 4(7)]

h  =  √333

h = 18.25 cm

Example 3 :

A girl wishes to prepare birthday caps in the form of right circular cones for her birthday party, using a sheet of paper whose area is 5720 cm², how many caps can be made with radius 5 cm and height 12 cm.

Solution :

r = 5 cm, height of cap  =  12 cm

slant height =  √(r² + h²)

 =  √(5² + 12²)

 =  √(25 + 144)

h  =  √169

h = 13

Area of sheet  =  5720 cm²

Curved surface area of one cap  =  Πrl

  =  (22/7) ⋅ 5 ⋅ 13  -----(1)

Required number of cups  =  5720 / [ (22/7) ⋅ 5 ⋅ 13]

=  (5720 ⋅ 7)/(22 ⋅ 5 ⋅ 13)

=  28 cups

Example 4 :

The ratio of the radii of two right circular cones of same height is 1:3. Find the ratio of their curved surface area when the height of each cone is 3 times the radius of the smaller cone.

Solution :

r₁  =  1, r₂  =  3

Height of 1^st cone  =  3(radius of smaller cone)

  =  3(1)  =  3

Height of 2^nd cone  =  3(radius of smaller cone)

  =  3(1)  =  3

Slant height of 1st cone  =   √(r² + h²)

=   √(1² + 3²)

=   √10

Slant height of 1st cone  =   √(r² + h²)

=   √(3² + 3²)

=   √18  =  3√2

Curved surface area  =  Πrl

Πr₁l₁ : Πr₁l₁

1√10 : 3 (3√2)

√10 : 9√2

√5 : 9

Example 5 :

Total surface area of a cone whose radius as p/2 and slant height as 2l is:

(a) 2 Π p(l + p)    (b) Πp(l + p/4)    (c)   Π p(1 + p)  (d) 2πpl

Solution :

Total surface area of cone = Πr (l + r)

Radius = p/2, slant height = 2l

= Π (p/2) (2l + (p/2)))

Factoring 2 from the bracket, we get

= Π (p/2) x 2(l + (p/4))

= Π p (l + (p/4))

So, option b is correct.

Example 6 :

If the slant height of a cone 12cm and radius of the base is 14 cm, then the total surface area is

Solution :

Slant height (l) = 12 cm

radius (r) = 14 cm

Total surface area = Πr (l + r)

= (22/7) x 14 (12 + 14)

= 22 x 2 x 26

= 1144 cm²

Example 7 :

The radius and height of a cone are in the ratio 4:3. The area of the base is 154 cm². Find the curved surface area.

Solution :

Radius and height are in the ratio 4 : 3

Radius = 4x and height = 3x

Area of base = Πr² 

(22/7) x r² = 154 cm²

r² = 154 x (7/22)

r² = 49

r = 7 cm

4x = 7

x = 7/4

height (h) = 3(7/4) = 21/4

Curved surface area of cone = Πrl

l = √r² + h²

l = √7² + (21/4)²

= √49 + (441/16)

= √1225/16

l = 35/4

Curved surface area = (22/7) x 7 x (35/4)

= 192.5 cm²

Example 8 :

There are two cones, the curved surface area of one cone is twice that of the other. The slant height of later is twice that of the former. Find the ratio of their radii.

Solution :

Let r, h and l be radius, height and slant height of the smaller cone.

Let R, H and L be radius, height and slant height of the larger cone.

ΠRL = 2(Πrl)

l = 2L

RL = 2( r(2L) )

RL = 4rL

R = 4r

R/r = 4/1

R : r = 4 : 1

So, the ratio between radius of larger and smaller circle is 4 : 1.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.