CUBOIDS

About "Cuboids"

Cuboids :

It is a three dimensional solid having six rectangular faces.

Example: Bricks, Books etc.,

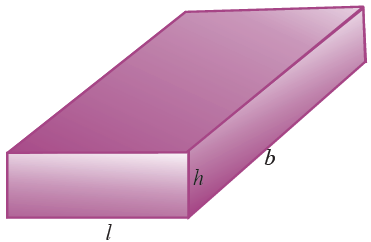
Surface area of a cuboid

Let l, b and h be the length, breadth and height of a cuboid respectively. To find the

total surface area, we split the faces into three pairs.

(i) The total area of the front and back faces is

lh + lh  =  2lh square units.

(ii) The total area of the side faces is

bh + bh  =  2bh square units.

(iii) The total area of the top and bottom faces is

lb + lb  =  2lb square units.

Volume of cuboid

If the length, breadth and height of a cuboid are l, b and h respectively, then the volume V of the cuboid is given by the formula

V  =  l ⋅ b ⋅ h cubic units

Example problems of surface area and volume of cuboid

Example 1 :

Find the total surface area of a cuboid whose length, breadth and height are 20 cm, 12 cm and 9 cm  respectively.

Solution :

Given that l = 20 cm, b = 12 cm, h = 9 cm

T.S.A = 2 (lb + bh + lh)

  =  2[(20 ⋅ 12) + (12 ⋅ 9) + (20 ⋅ 9)]

  =  2(240 + 108 + 180)

  =  2 (528)

  =  1056 cm²

Example 2 :

Find the L.S.A of a cuboid whose dimensions are given by 3m ⋅ 5m ⋅ 4m

Solution :

Given that l  =  3 m, b  =  5 m, h  =  4 m

L.S.A  =  2h (l + b)

  =  2(4) (3 + 5)

  =  8 (8)

  =  64 sq. m

Hence the required lateral surface area is 64 sq. m.

Example 3 :

Find the volume of a cuboid whose dimensions are given by 11 m, 10 m and 7 m.

Solution :

Given that l = 11 m, b = 10 m, h = 7 m

Volume of cuboid  =  lbh

  =  11 ⋅ 10 ⋅ 7

  =  770 cu.m.

Example 4 :

Two cubes each of volume 216 cm³ are joined to form a cuboid as shown in the figure.

Find the T.S.A of the resulting cuboid.

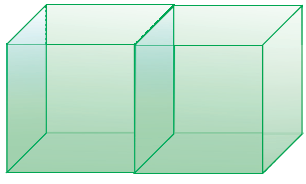
Solution :

Let the side of each cube be a. Then a³  =  216

 a = ∛216 = 6 cm

Now the two cubes of side 6 cm are joined to form a cuboid.

So,

l = 6 + 6 = 12 cm, b = 6 cm, h = 6 cm

Total surface area  =  2 (lb + bh + lh)

  =  2 [(12 ⋅ 6) + (6 ⋅ 6) + (12 ⋅ 6)]

  =  2 [72 + 36 + 72]

  =  2 ⋅ 180 

=  360 cm²

Hence the required total surface area is 360 cm²

After having gone through the stuff given above, we hope that the students would have understood "Cuboid". 

Apart from the stuff given above, if you want to know more about "Cuboid".

Apart from the stuff given in this section, if you need any other stuff in math, please use our google custom search here.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.