CUBIC UNITS

A cubic unit is a unit of volume in the International System of Units (SI). This concept is fundamental to much of geometry and physical science. As its name suggests, a unit of cubic dimension refers to the volume of a cube whose sides measure exactly one unit.

The most basic unit of volume in the metric system is the cubic meter (m³). One cubic meter is the volume of a cube with sides measuring one meter on each edge. Other units derived from the cubic meter include the cubic centimeter (cm³), the cubic millimeter (mm³), and the cubic kilometer (km³).

Understanding cubic units forms a valuable part of mathematics and physical science education because it applies to real-world applications such as measuring the capacity, volume, or quantity of a substance or material. For instance, when you calculate the volume of a shipping box, you would measure it in cubic units.

Cubic units also help us in understanding the geometry of three-dimensional objects. A cube is a regular three-dimensional shape where all sides are equal, and all angles are right angles. It's one of the simplest and most familiar forms to work with when learning about volume and cubic units.

When finding the volume of a cube, you simply have to calculate the space a cube occupies, which is equal to the side length raised to the power of three. For example, if the side length of the cube is 3 units, the volume would be 3³ = 27 cubic units.

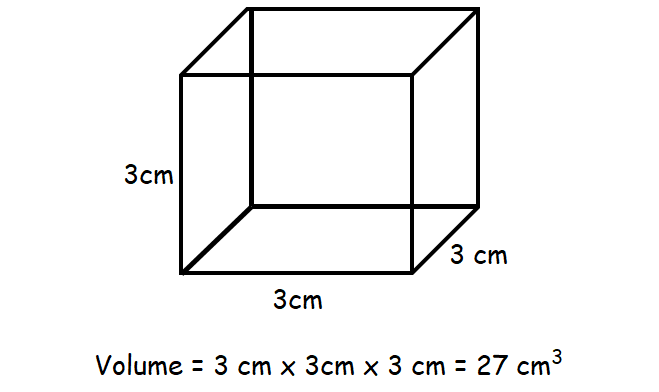
Meanwhile, in a cubic centimeter scenario, if a box measures 2 centimeters on all sides, it would have a volume of 2³ = 8 cubic centimeters. The same concept applies to other cubes, like ones measured in kilometers, millimeters, feet, etc.

Apart from cubes, it's also possible to use cubic units to calculate the volume of other three-dimensional shapes. For instance, the volume of a cylinder or a prism would be the base area times the height. These measurements would also be in cubic units, reflecting the three-dimensional nature of the shapes.

Another interesting note regarding cubic units, they also help enhance our understanding of the universe. For example, when scientists measure the size or volume of stars, planets, or galaxies, they use cubic units. This significantly highlights the application of cubic units in astronomy.

Moreover, cubic units come in handy in measuring substances that can take the shape of their containers, like liquids or gases. Cubic units allow scientists to measure and define these substances in a coherent and standardized manner, which plays a crucial role in scientific experiments and industrial applications.

In the field of engineering and architecture, cubic units measure the amount of concrete, gravel, or other materials needed to complete a project. This highlights the significant use of cubic units in the construction industry.

In the healthcare sector, medical professionals use cubic units to measure the volume of liquids or solid materials in the human body. For instance, a medication dose may be specified in cubic millimeters (mm³) or cubic centimeters (cm³).

Another essential factor to note is the conversion between different cubic units. Typically based on the factor of 10, this allows students and professionals to easily transition between metric units.

For example, there are 1,000,000 cubic millimeters (mm³) in a cubic decimeter (dm³), reflecting the metric system framework. This system of measurement is decimal-based, which is why it is straightforward to convert between units.

In not so straightforward scenarios is the conversion of cubic units in the Imperial or Customary system, such as cubic feet, cubic yards, and cubic inches. Conversion factors between these are not consistent and require memorization or a reference table.

Despite these challenges, understanding cubic units and their conversions is integral to science, engineering, and daily life. A grasp of these units and measurements can play a crucial role in problem-solving and rational decision-making in numerous professional and daily scenarios.

On a more philosophical note, by understanding cubic units, we not only comprehend the physical dimension of objects but also appreciate the underlying mathematical harmony and precision in the universe.

In a nutshell, the understanding of cubic units allows us to deal with volume measurements more efficiently - in schoolwork, professional work, or even when doing simple tasks like baking or interior decoration at home.

To conclude, the concept of cubic units might seem trivial at first, but when deeply understood, it opens doors to a universe of precise measurements, rational understanding, and appreciation for the volumetric wonders of the physical world that surrounds us.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.