CUBES AND CUBE ROOTS

Cubes

If you multiply a number by itself and then by itself again, the result is a cube number. Th is means that a cube number is a number that is the product of three identical numbers. If n is a number, its cube is represented by n³.

Cube numbers can be represented visually as 3D cubes comprising of single unit cubes. Cube numbers are also called as perfect cubes.

The perfect cubes of natural numbers are 1, 8, 27, 64, 125, 216, ... and so on.

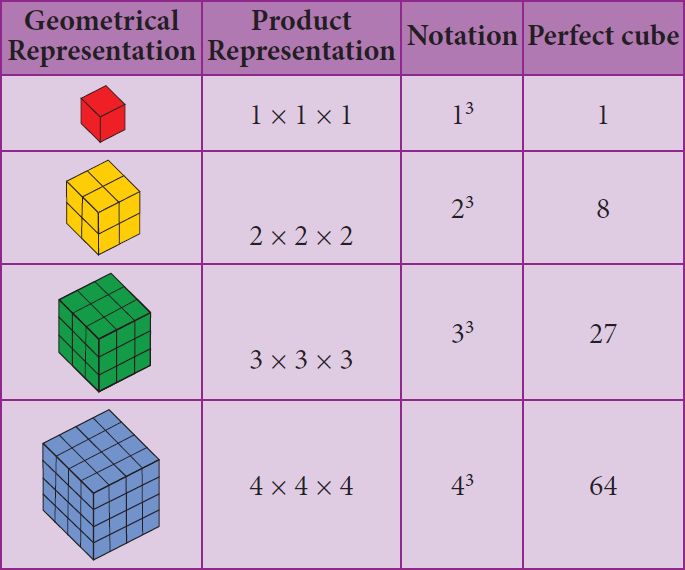
Properties of Cubes of Numbers

Property 1 :

The cube of a positive number is positive.

Example :

= 5³

= 5 x 5 x 5

= 125

Property 2 :

The cube of a negative number is negative.

Example :

= (-2)³

= (-2) x (-2) x (-2)

= (+4) x (-2)

= -8

Property 3 :

The cube of every even number is even.

Example :

= 4³

= 4 x 4 x 4

= 64 is even

Property 4 :

The cube of every odd number is odd.

Example :

= 3³

= 3 x 3 x 3

= 27 is even

Property 5 :

If a natural number ends with 0, 1, 4, 5, 6 or 9, its cube also ends with the same 0,1, 4, 5, 6 or 9 respectively.

Example :

10³ = 10 x 10 x 10 = 1000

11³ = 11 x 11 x 11 = 1331

14³ = 14 x 14 x 14 = 2744

15³ = 15 x 15 x 15 = 3375

16³ = 16 x 16 x 16 = 4096

19³ = 19 x 19 x 19 = 6859

Property 6 :

If a natural number ends with 2 or 8, its cube ends with 8 or 2 respectively.

Example :

12³ = 12 x 12 x 12 = 1728

18³ = 18 x 18 x 18 = 5832

Property 7 :

If a natural number ends with 3 or 7, its cube ends with 7 or 3 respectively.

Example :

13³ = 13 x 13 x 13 = 2197

17³ = 17 x 17 x 17 = 4913

Property 8 :

The sum of the cubes of first n natural numbers is equal to the square of their sum.

1³ + 2³ + 3³ + .......... + n³ = (1 + 2 + 3 + .......... + n)²

Example :

1³ + 2³ + 3³ + 4³ = 1 + 8 + 27 + 64 = 100 ----(1)

(1 + 2 + 3 + 4)²  = (10)² = 100 ----(2)

From (1) and (2),

1³ + 2³ + 3³ + 4³ = (1 + 2 + 3 + 4)²

Cube Root

The cube root of a number is the value that when cubed gives the original number.

For example, the cube root of 27 is 3 because when 3 is cubed we get 27.

Notation :

The cube root of a number x is denoted as

Here are some more cubes and cube roots :

Example 1 :

Is 400 a perfect cube?

Solution :

By prime factorisation, we have

400 = 2 × 2 × 2 × 2 × 5 × 5

400 = (2 × 2 × 2) × 2 × 5 × 5

There is only one triplet. To make further triplets, we will need two more 2’s and one more 5. Therefore, 400 is not a perfect cube.

Example 2 :

Find the smallest number by which 675 must be multiplied to obtain a perfect cube.

Solution :

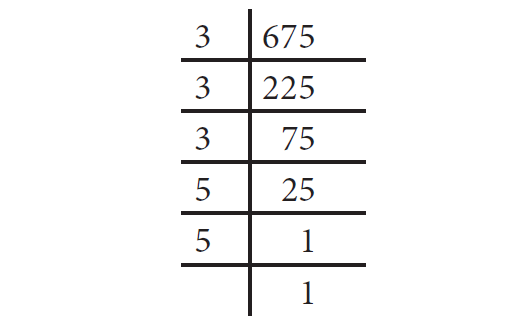
By prime factorisation, we have

675 = 3 × 3 × 3 × 5 × 5 ----(1)

Th ere is only one triplet. To make further triplets, we will need two more 2’s and one more 5. Therefore, 400 is not a perfect cube.

Grouping the prime factors of 675 as triplets, we are left over with 5 × 5.

We need one more 5 to make it a perfect cube.

To make 675 a perfect cube, multiply both sides of (1) by 5.

675 × 5 = 3 × 3 × 3 × 5 × 5 × 5

3375 = 3 × 3 × 3 × 5 × 5 × 5

Now, 3375 is a perfect cube. Th us, the smallest required number to multiply 675 such that the new number perfect cube is 5.

Example 3 :

Find the cube root of 27000.

Solution :

By prime factorisation, we have

27000 = 2 × 2 × 2 × 3 × 3 × 3 × 5 × 5 × 5

Cube root of 27000 :

Example 4 :

Evaluate :

Solution :

Example 5 :

Evaluate :

Solution :

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.