CUBES AND CUBE ROOTS WORKSHEET

Problem 1 :

Is the cube of a positive number positive or negative? Give an example.

1. Answer :

The cube of a positive number is positive.

Example :

= 6³

= 6 x 6 x 6

= 216

Problem 2 :

Is the cube of a negative number positive or negative? Give an example.

2. Answer :

The cube of a negative number is negative.

Example :

= (-5)³

= (-5) x (-5) x (-5)

= (+25) x (-5)

= -125

Problem 3 :

Is the cube of every even number even or odd? Give an example.

3. Answer :

The cube of every even number is even.

Example :

= 2³

= 2 x 2 x 2

= 8 is even

Problem 4 :

Is the cube of every odd number even or odd? Give an example.

4. Answer :

The cube of every odd number is odd.

Example :

= 7³

= 7 x 7 x 7

= 343 is even

Problem 5 :

If a natural number ends with one of the digits 0, 1, 4, 5, 6 or 9,  does its cube also end with the same digit? Give examples.

5. Answer :

If a natural number ends with 0, 1, 4, 5, 6 or 9, its cube also ends with the same 0, 1, 4, 5, 6 or 9 respectively.

Example :

10³ = 10 x 10 x 10 = 1000

11³ = 11 x 11 x 11 = 1331

14³ = 14 x 14 x 14 = 2744

15³ = 15 x 15 x 15 = 3375

16³ = 16 x 16 x 16 = 4096

19³ = 19 x 19 x 19 = 6859

Problem 6 :

If a natural number ends with the digit 2 or 8, in what digit does it cube end with? Given example.

6. Answer :

If a natural number ends with 2 or 8, its cube ends with 8 or 2 respectively.

12³ = 12 x 12 x 12 = 1728

18³ = 18 x 18 x 18 = 5832

Problem 7 :

If a natural number ends with the digit 3 or 7, in what digit does it cube end with? Give Example

7. Answer :

If a natural number ends with 3 or 7, its cube ends with 7 or 3 respectively.

Example :

13³ = 13 x 13 x 13 = 2197

17³ = 17 x 17 x 17 = 4913

Problem 8 :

How will you find the sum of cubes of first n natural numbers? And also, find the sum of cubes of first 5 natural numbers. 

8. Answer :

The sum of the cubes of first n natural numbers is equal to the square of their sum.

1³ + 2³ + 3³ + .......... + n³ = (1 + 2 + 3 + .......... + n)²

Sum of cubes of first 5 natural numbers :

= 1³ + 2³ + 3³ + 4³ + 5³ 

= (1 + 2 + 3 + 4 + 5)²

= 15²

= 225

Problem 9 :

Will a perfect cube end with two zeros? Give an example.

9. Answer :

No, a perfect cube will not end with two zeros.

For example, 100 ends with two zeros, but it is not a perfect cube. 1000 is a perfect cube, but it ends with three zeros. 

Problem 10 :

How many digits may the cube of a two digit number have?

10. Answer :

The cube of a two digit number may have 4 or 5 or 6 digits in it.

The smallest two digit number is 10.

10³ = 1000 (four digits)

The largest two digit number is 99.

99³ = 970299 (six digits)

Problem 11 :

Is 400 a perfect cube?

11. Answer :

No. 400 is not a perfect cube. Because it ends with two zeros.

Problem 12 :

Find the smallest number by which 675 must be multiplied to obtain a perfect cube.

12. Answer :

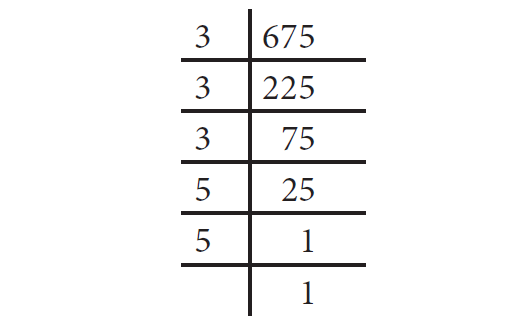
By prime factorisation, we have

675 = 3 × 3 × 3 × 5 × 5 ----(1)

Th ere is only one triplet. To make further triplets, we will need two more 2’s and one more 5. Therefore, 400 is not a perfect cube.

Grouping the prime factors of 675 as triplets, we are left over with 5 × 5.

We need one more 5 to make it a perfect cube.

To make 675 a perfect cube, multiply both sides of (1) by 5.

675 × 5 = 3 × 3 × 3 × 5 × 5 × 5

3375 = 3 × 3 × 3 × 5 × 5 × 5

Now, 3375 is a perfect cube. Th us, the smallest required number to multiply 675 such that the new number perfect cube is 5.

Problem 13 :

Find the cube root of 64000.

13. Answer :

By prime factorisation, we have

64000 = 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 5 × 5 × 5

Cube root of 64000 :

Problem 14 :

Evaluate :

14. Answer :

Problem 15 :

Evaluate :

15. Answer :

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.