CUBE ROOTS AND RADICALS

Finding cube root of a number is the inverse operation of finding cube.

The radical of a number is the same as the root of a number. The root may be square root or cube root and so on.

So, cube root is also a radical with index 3.

Example 1 :

Find the cube root of 512.

Solution :

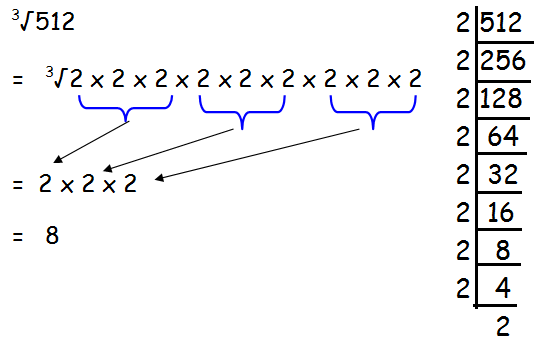
Hence cube-root of 512 is 8.

Example 2 :

Find the cube-root of 27 x 64

Solution :

  =  ∛27 x 64 

We can write 27 as 3 x 3 x  3, like wise 64 as 4 x 4 x 4.

  =  ∛3 x 3 x 3 x 4 x 4 x 4

  =  3 x 4

  =  12

Hence the answer is 12.

Example 3 :

Find the cube-root of 125/216.

Solution :

Here we need to find the cube-root for a fraction. For that, split the numerator and denominator as much as possible.

  =  ∛125/216

125  =  5 x 5 x 5 and 64  =  4 x 4 x 4

  =  ∛(5 x 5 x 5) /(4 x 4 x 4)

Since we have cube-root, we need to take one for each three same terms.

  =  5/4

Hence the cube root of 125/216 is 5/4.

Example 4 :

Find the cube-root of -512/1000.

Solution :

Here we need to find the cube-root for a fraction. In the cube-root we have negative sign.

Whenever we have negative sign inside the cube-root, the answer must have negative sign.

  =  ∛512/1000

512  =  8 x 8 x 8 and 1000  =  10 x 10 x 10

  = - ∛(8 x 8 x 8)/(10 x 10 x 10)

Since we have cube-root, we need to take one for each three same terms.

  =  - 8/10

If it is possible, we may simplify

  =  - 4/5

Hence the cube-root of ∛-512/1000 is -4/5.

Example 5 :

Find the cube-root of 0.027.

Solution :

Here we need to find the cube-root for a decimal. 

First let us convert the given decimal as fraction. For that, we have to multiply and divide by 1000.

0.027 x  (1000/1000)  =  27/1000

∛0.027  =  ∛27/1000

  =  ∛(3 x 3 x 3)/(10 x 10 x 10)

  =  3/10

Hence the cube-root of ∛0.027 is 3/10.

Example 6 :

Simplify the following radical terms

4√3, 18√2, -3√3, 15√2

Solution :

  =  4√3 + 18√2 - 3√3 + 15√2 

To simplify the above terms, we need to combine the like terms

  =  4√3  - 3√3 + 18√2 + 15√2

  =  (4 - 3) √3 + (18 + 15) √2

  =  1√3 + 33√2

  =  √3 + 33√2

Example 7 :

Simplify the following radical terms

2∛2, 24∛2, - 4∛2

Solution :

  =  2∛2 + 24∛2 - 4∛2

  =  (2 + 24 - 4) ∛2

 =  22 ∛2

Example 8 :

Multiply ∛13 x ∛5 

Solution :

  =  ∛13 x ∛5 

Since the index of both root terms are same, we can write only one root sign and multiply the numbers.

  =  ∛(13 x 5) 

  =  ∛65

Example 9 :

Multiply 15√54 ÷ 3√6

Solution :

  =  15√54 ÷ 3√6

Since the index of both root terms are same, we can write only one root and divide the numbers.

=  (15/3)√(54/6)

=  5√9  ==>  5√(3 x 3)  ==> 5 x 3  ==> 15

Example 10 :

Multiply (48)^1/4 ÷ (72)^1/8

Solution :

  =  (48)^1/4 ÷ (72)^1/8

Since the index of the above  root terms are not same, we need to convert the power 1/4 as 1/8.

  =  (48)^{(1/4) x (2/2)} ÷ (72)^1/8

  =  (48)^(2/8) ÷ (72)^1/8

  =  48^{2 (1/8)} ÷ (72)^1/8

=  [(48 x 48) ÷ (72)]^1/8

=  [2304 ÷ 72]^1/8

=  (32)^1/8

Example 11 :

Is 1188 a perfect cube? If not, by which smallest natural number should 1188 be divided so that the quotient is a perfect cube?

Solution :

Decomposing 1188,

= 2 x 2 x 3 x 3 x 3 x 11

1188 is not a perfect cube, to group them as three same values we need ignore one 2 and two 11's. So, 

= 2 x 11 x 11

That is, 242 is to be divided to make 1188 as perfect cube.

Example 12 :

A cubical box has a volume of 512000 cubic cm. What is the length of the side of box?

Solution :

Volume of cubical box = 512000 cubic cm

Let a be the side length of cube

a³ = 512000

a = ∛512000

= ∛(8 x 8 x 8 x 10 x 10 x 10)

= 8 x 10

= 80 cm

So, the side length of the cube is 80 cm.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.