SOLVING LINEAR EQUATIONS USING CROSS MULTIPLICATION METHOD
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
This is one of the methods we use to solve system of linear equations.
Let us consider the following system of linear equations.
a1x + b1y + c1 = 0
a2x + b2y + c2 = 0
We have to write the coefficients of the equations and do cross multiplication as shown below.
We write the coefficient of y and constant term and two more columns by repeating the coefficients of x and y as follows.
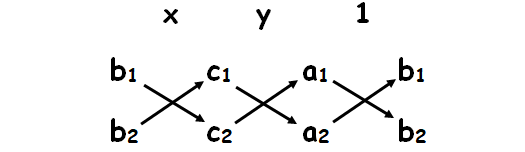
The result is given by
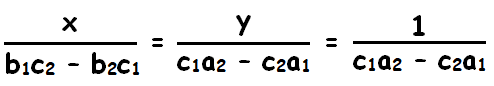
The solution is
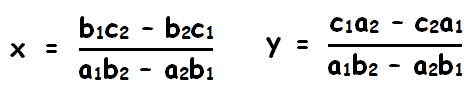
Solve the following system of equations using cross multiplication method.
Problem 1 :
3x + 4y = 24, 20x - 11y = 47
Solution :
3x + 4y - 24 = 0 ----- (1)
20x - 11y - 47 = 0 ----- (2)
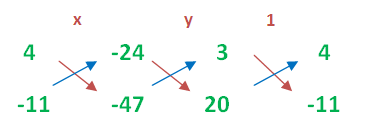
x/(-188-264) = y/(-480 -(-141)) = 1/(-33-80)
x/(-452) = y/(-480+141)) = 1/(-33-80)
x/(-452) = y/(-339) = 1/(-113)
|
x/(-452) = 1/(-113) x = (-452)/(-113) x = 4 |
y/(-339) = 1/(-113) y = (-339)/(-113) y = 3 |
So, the solution is (4, 3).
Problem 2 :
0.5x + 0.8y = 0.44 , 0.8x + 0.6y = 0.5
Solution :
0.5x+0.8y = 0.44 ----- (1)
0.8x+0.6y = 0.5 ----- (2)
To make the decimal numbers into integers, we have to multiply the first equation by 100 and the second equation by 10.
50x+80y-44 = 0 ----- (1)
8x+6y-5 = 0 ----- (2)
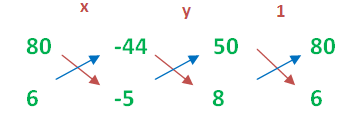
x/(-400-(-264)) = y/(-352 -(-250)) = 1/(300-640)
x/(-400+264) = y/(-352+250)) = 1/(-340)
x/(-136) = y/(-102) = 1/(-340)
|
x/(-136) = 1/(-340) x = (-136)/(-340) x = 0.4 |
y/(-102) = 1/(-340) y = (-102)/(-340) y = 0.3 |
So, the solution is (0.4, 0.3).
Problem 3 :
(3x/2) - (5y/3) = -2 , (x/3) + (y/2) = 13/6
Solution :
9x - 10y = -12
(2x + 3y)/6 = 13/6
9x-10y+12 = 0 ----- (1)
2x+3y-13 = 0 ----- (2)
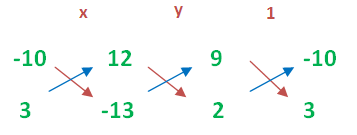
x/(130-36) = y/(24 -(-117)) = 1/(27-(-20))
x/(94) = y/(24+117)) = 1/(27+20)
x/(94) = y/(141) = 1/(47)
|
x/(94) = 1/(47) x = 94/47 x = 2 |
y/(141) = 1/(47) y = (141)/(47) y = 3 |
So, the solution is (2, 3).
Problem 4 :
(5/x)-(4/y) = -2 , (2/x)+(3/y) = 13
Solution :
Let 1/x = a and 1/y = b
5a-4b = - 2
2a+3 b = 13
5a - 4b + 2 = 0 ----- (1)
2a + 3b - 13 = 0 ----- (2)
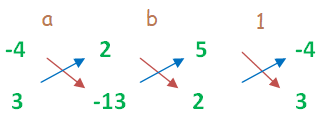
a/(52-6) = b/(4 -(-65)) = 1/(15-(-8))
a/46 = b/(4 +65) = 1/(15+8)
a/(46) = b/(69) = 1/(23)
|
a/(46) = 1/(23) a = 46/23 a = 2 |
b/(69) = 1/(23) b = 69/23 b = 3 |
x = 1/2 and y = 1/3
So, the solution is (1/2, 1/3).
Problem 5 :
Ms. Kitts works at a music store. Last week she sold 6 more than 3 times the number of CDs that she sold this week. Ms. Kitts sold a total of 110 CDs over the 2 weeks. Which system of equations can be used to find x the number of CDs she sold last week and y the number of CDs she sold this week ?
Solution :
Number of CDs sold last week = x
Number of CDs sold this week = y
x + y = 110 -------(1)
x = 3y + 6 -------(2)
x + y - 110 = 0
x - 3y - 6 = 0
1 -110 1 1
-3 -6 1 -3
x/(-6 - 330) = y/(-110 + 6) = 1/(-3 - 1)
x/-336 = y/-104 = 1/-4
Equating each fractions by -1/4, we get
x = -324/-4
x = 81
y/-104 = -1/4
y = -104/-4
y = 263
Number of CDs sold last week = 84
Number of CDs sold this week = 26
Problem 6 :
The length of the rectangle is equal to triple the width. Which system of equations can be used to find the dimensions of the rectangle if the perimeter is 86 centimeters ?
Solution :
Let x be the length and width be y
x = 3y ------(1)
2x + 2y = 86
Dividing by 2, we get
x + y = 43 -----(2)
x - 3y = 0
x + y - 43 = 0
-3 0 1 -3
1 -43 1 1
Doing cross multiplication, we get
x/(129 - 0) = y/(0 + 43) = 1/(1 + 3)
x/129 = y/43 = 1/4
Equating each fraction with 1/4, we get
x/129 = 1/4
x = 129/4
y/43 = 1/4
y = 43/4
Problem 7 :
At a restaurant the cost for a taco and small glass of milk is $2.10. The cost for 2 tacos and 3 small glasses of milk is $5.15. Which pair of equations can be used to determine x the cost of a taco and y the cost of small glass of milk ?
Solution :
x - cost of taco and y - cost of cost of small glass of milk
x + y = 2.10
2x + 3y = 5.15
x + y - 2.10 ------(1)
2x + 3y - 5.15 -----(2)
1 -2.10 1 1
3 -5.15 2 3
x/(-5.15 + 6.3) = y/(-4.20 + 5.15) = 1/(3 - 2)
x/1.15 = y/0.95 = 1/1
x = 1.5 and y = 0.95
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
©All rights reserved. onlinemath4all.com
Recent Articles
-
SAT Math Practice
Dec 05, 25 04:04 AM
SAT Math Practice - Different Topics - Concept - Formulas - Example problems with step by step explanation -
10 Hard SAT Math Questions (Part - 37)
Dec 03, 25 07:02 AM
10 Hard SAT Math Questions (Part - 37) -
Factorial Problems and Solutions
Dec 02, 25 09:27 AM
Factorial Problems and Solutions

