CONVERTING REPEATING DECIMALS TO FRACTIONS
About "Converting repeating decimals to fractions"
"Converting repeating decimals to fractions" is a much required stuff for the children who study high school math.
Here, we are going to see, how to convert repeating decimals to mixed fractions step by step.
Steps involved
Step 1 :
Let x = Given decimal number
For example,
If the given decimal number is 2.0343434.........
then, let x = 2.0343434...........
Step 2 :
Identify the repeated pattern
For example,
In 2.0343434..........., the repeated pattern is 34
(Because 34 is being repeated)
Step 3 :
Identify the first repeated pattern and second repeated pattern as as explained in the example given below.
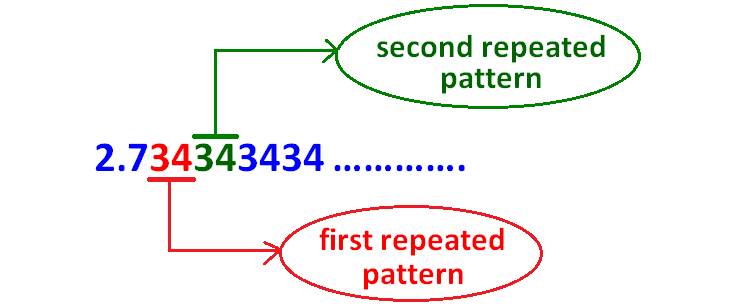
Step 4 :
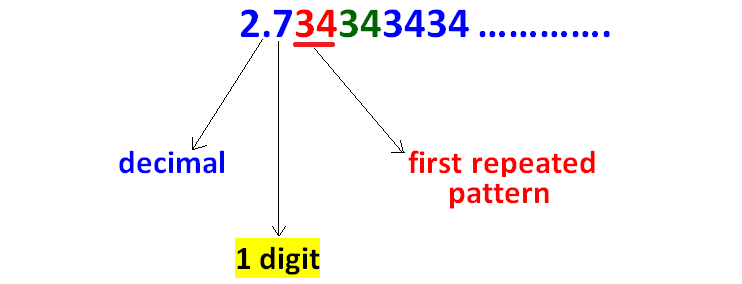
Count the number of digits between the decimal point and first repeated pattern as given in the picture below.
Step 5 :
Since there is 1 digit between the decimal point and the first repeated pattern, we have to multiply the given decimal by 10 as given in the picture below.
(If there are two digits -----------> multiply by 100,
three digits -----------> multiply by 1000 and so on )
Note : In (1), we have only repeated patterns after the decimal.
Step 6 :
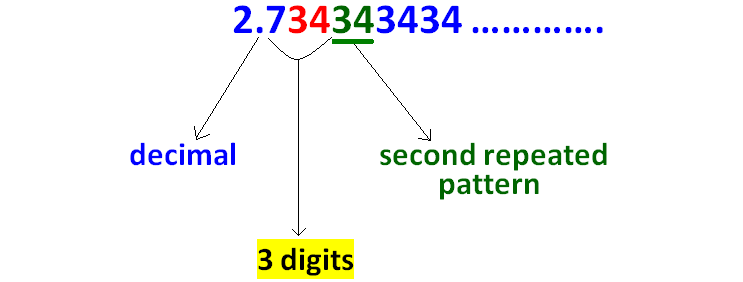
Count the number of digits between the decimal point and second repeated pattern as given in the picture below.
Step 7 :
Since there are 3 digits between the decimal point and the second repeated pattern, we have to multiply the given decimal by 1000 as given in the picture below.
Note : In (2), we have only repeated patterns after the decimal.
Step 8 :
Now, we have to subtract the result of step 5 from step 7 as given in the picture below.
Now we got the fraction which is equal to the given decimal
Some more problems
To have better understanding on "Converting repeating decimals to fractions", let us look at some problems.
Problem 1 :
Covert the given repeating decimal into fraction
32.03256256256..........
Solution :
Let X = 32.03256256256.............
Here, the repeated pattern is 256
No. of digits between the 1st repeated pattern and decimal = 2
So, multiply the given decimal by 100. Then, we have
100X = 3203.256256256...............----------(1)
No. of digits between the 2nd repeated pattern and decimal = 5
So, multiply the given decimal by 100000. Then, we have
100000X = 3203256.256256256...............----------(2)
(2) - (1) --------> 99900X = 3200053
X = 3200053 / 99900
Hence, 32.03256256256.......... = 3200053 / 99900
Let us look at the next problem on "Converting repeating decimals to fractions".
Problem 2 :
Covert the given repeating decimal into fraction
0.01232222........
Solution :
Let X = 0.01232222.............
Here, the repeated pattern is 2
No. of digits between the 1st repeated pattern and decimal = 4
(Here, the first repeated pattern starts after four digits of the decimal)
So, multiply the given decimal by 10000. Then, we have
10000X = 123.2222...............----------(1)
No. of digits between the 2nd repeated pattern and decimal = 5
So, multiply the given decimal by 100000. Then, we have
100000X = 1232.2222...............----------(2)
(2) - (1) --------> 90000X = 1109
X = 1109 / 90000
Hence, 0.01232222........... = 1109 / 90000
Let us look at the next problem on "Converting repeating decimals to fractions".
Problem 3 :
Covert the given repeating decimal into fraction
2.03323232..........
Solution :
Let X = 2.03323232.............
Here, the repeated pattern is 32
No. of digits between the 1st repeated pattern and decimal = 2
(Here, the first repeated pattern starts after two digits of the decimal)
So, multiply the given decimal by 100. Then, we have
100X = 203.323232...............----------(1)
No. of digits between the 2nd repeated pattern and decimal = 4
So, multiply the given decimal by 10000. Then, we have
10000X = 20332.323232...............----------(2)
(2) - (1) --------> 9900X = 20129
X = 9900 / 20129
Hence, 2.03323232.......... = 9900 / 20129
Let us look at the next problem on "Converting repeating decimals to fractions".
Problem 4 :
Covert the given repeating decimal into fraction
0.252525..........
Solution :
Let X = 0.252525.............
Here, the repeated pattern is 25
No. of digits between the 1st repeated pattern and decimal = 0
So, multiply the given decimal by 1. Then, we have
X = 0.252525...............----------(1)
No. of digits between the 2nd repeated pattern and decimal = 2
So, multiply the given decimal by 100. Then, we have
100X = 25.252525...............----------(2)
(2) - (1) --------> 99X = 25
X = 25 / 99
Hence, 0.252525.......... = 25 / 99
Let us look at the next problem on "Converting repeating decimals to fractions".
Problem 5 :
Covert the given repeating decimal into fraction
3.3333..........
Solution :
Let X = 3.3333.............
Here, the repeated pattern is 3
No. of digits between the 1st repeated pattern and decimal = 0
(Here, the first repeated pattern is "3" which comes right after the decimal point)
So, multiply the given decimal by 1. Then, we have
X = 3.3333...............----------(1)
No. of digits between the 2nd repeated pattern and decimal = 1
(Here, the second repeated pattern is "3" which comes one digit after the decimal point)
So, multiply the given decimal by 10. Then, we have
10X = 33.3333...............----------(2)
(2) - (1) --------> 9X = 30
X = 30 / 9 = 10 / 3
Hence, 3.3333.............. = 10 / 9
Problem 6 :
Covert the given repeating decimal into fraction
1.023562562562..........
Solution :
Let X = 1.023562562562.............
Here, the repeated pattern is 562
No. of digits between the 1st repeated pattern and decimal = 3
So, multiply the given decimal by 1000. Then, we have
1000X = 1023.562562562...............----------(1)
No. of digits between the 2nd repeated pattern and decimal = 6
So, multiply the given decimal by 1000000. Then, we have
1000000X = 1023562.562562562...............----------(2)
(2) - (1) --------> 999000X = 1022538
X = 1022539 / 999000
Hence, 1.023562562562.......... = 1022539 / 999000
After having gone through the stuff and examples, we hope that the students would have understood, "How to convert repeating decimals into fractions"
Apart from the stuff and examples, if you want to know more about, "Converting repeating decimals to fractions", please click here.
Related Topics
Converting percent into fractions
Converting improper fractions into mixed fractions
Converting mixed fractions into improper fractions
Converting decimals into fractions
