CONVERTING RECURRING DECIMALS TO FRACTIONS

How to convert recurring decimals to fractions :

Step 1 :

Let x be the given decimal number. 

For example, x = 2.7343434..............

Step 2 : 

Identify the repeated pattern

In 2.7343434..........., the repeated pattern is 34

(Because 34 is being repeated)

Step 3 :

Identify the first repeated pattern and second repeated pattern as shown below.  

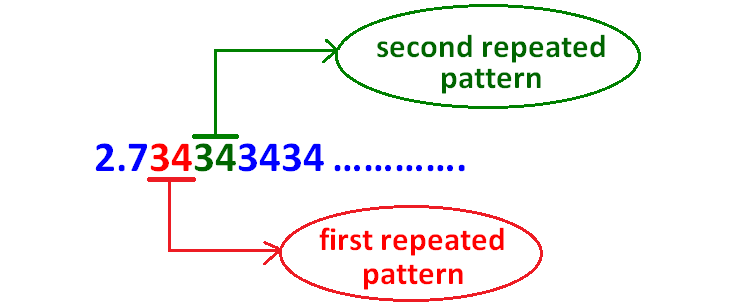
Step 4 :

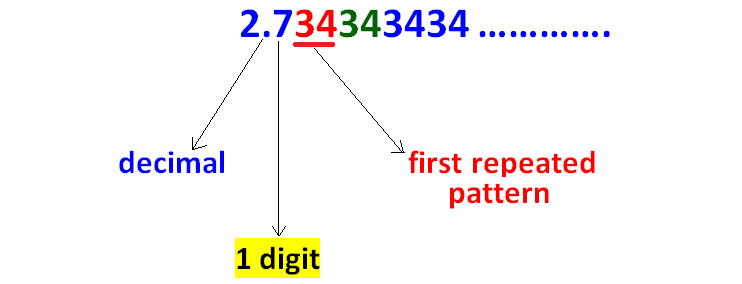
Count the number of digits between the decimal point and first repeated pattern as shown below.

Step 5 :

Because there is one digit between the decimal point and the first repeated pattern, we have to multiply the given decimal by 10. 

(If there are two digits, multiply by 100, three digits, multiply by 1000 and so on)

x  =  2.734343434....................

10x  =  10(2.734343434....................)

10x  =  27.34343434....................----(1)

Note :

In (1), we have only repeated patterns after the decimal.

Step 6 : 

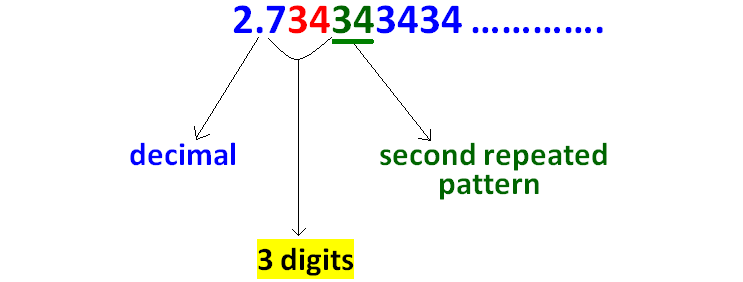
Count the number of digits between the decimal point and second repeated pattern as shown below. 

Step 7 :

Because there are three digits between the decimal point and the second repeated pattern, we have to multiply the given decimal by 1000. 

x  =  2.734343434....................

1000x  =  1000(2.734343434....................)

1000x  =  2734.343434....................----(2)

Note :

In (2), we have only repeated patterns after the decimal.

Step 8 :

Subtract the result of step 5 from step 7. 

So, 

2.7343434.............. =  2707/990

Solved Problems

Covert the recurring decimals to fractions :

Problem 1 :

32.03256256256..........

Solution : 

Let x = 32.03256256256.............

The repeated pattern is 256.

There are two digits between the decimal point and 1^st repeated pattern, that is 03. 

Multiply the given decimal number by 100.

100x  =  3203.256256256...............-----(1) 

There are five digits between the decimal point and the 2^nd repeated pattern, that is 03256. 

Multiply the given decimal number by 100000.

100000x  =  3203256.256256256...............-----(2)

Subtract (1) from (2).

99900x  =  3200053

x  =  3200053/99900

32.03256256256.......... =  3200053/99900

Problem 2 :

0.01232222........

Solution : 

Let x = 0.01232222.............

The repeated pattern is 2.

There are four digits between the decimal point and 1^st repeated pattern, that is 0123. 

Multiply the given decimal number by 10000. 

10000X  =  123.2222...............-----(1) 

There are five digits between the decimal point and the 2^nd repeated pattern, that is 01232.

Multiply the given decimal number by 100000.

100000x  =  1232.2222...............-----(2)

Subtract (1) from (2). 

90000x  =  1109

x  =  1109/90000

0.01232222........... =  1109/90000

Problem 3 :

2.03323232..........

Solution : 

Let x = 2.03323232.............

The repeated pattern is 32.

There are two digits between the decimal point and 1^st repeated pattern, that is 03. 

Multiply the given decimal number by 100. 

100x  =  203.323232...............-----(1) 

There are four digits between the decimal point and the 2^nd repeated pattern, that is 0332. 

Multiply the given decimal number by 10000. 

10000x  =  20332.323232...............-----(2)

Subtract (1) from (2).

9900x  =  20129

x  =  9900/20129

2.03323232.......... =  9900/20129

Problem 4 :

0.252525..........

Solution : 

Let x = 0.252525.............

The repeated pattern is 25.

There is no digit between the decimal point and 1^st  repeated pattern.

x  =  0.252525...............-----(1) 

There are two digits between the decimal point and the 2^nd repeated pattern, that is 25. 

Multiply the given decimal number by 100.

100x  =  25.252525...............-----(2)

Subtract (1) from (2).

99x  =  25

x  =  25/99

0.252525.......... =  25/99

Problem 5 :

3.3333..........

Solution : 

Let x = 3.3333.............

The repeated pattern is 3.

There is no digit between the decimal point and 1^st  repeated pattern.

x  =  3.3333...............-----(1) 

There is one digit between the decimal point and the 2^nd repeated pattern, that is 3. 

Multiply the given decimal number by 10. 

10x  =  33.3333...............-----(2)

Subtract (1) from (2).

9x  =  30

x  =  30/9

x  =  10/3

3.3333.............. =  10/3

Problem 6 :

1.023562562562..........

Solution : 

Let x = 1.023562562562.............

The repeated pattern is 562.

There are three digits between the decimal point and 1^st repeated pattern, that is 023. 

Multiply the given decimal number by 1000.

1000x  =  1023.562562562...............-----(1) 

There are six digits between the decimal point and the 2^nd repeated pattern, that is 023562. 

Multiply the given decimal number by 1000000. 

1000000x  =  1023562.562562562...............-----(2)

Subtract (1) from (2). 

999000x  =  1022538

x  =  1022539/999000 

1.023562562562.......... =  1022539/999000

Apart from the stuff given above, if you need any other stuff in math, please use our google custom search here.

If you have any feedback about our math content, please mail us : 

v4formath@gmail.com

We always appreciate your feedback. 

You can also visit the following web pages on different stuff in math. 

WORD PROBLEMS

HCF and LCM  word problems

Word problems on simple equations 

Word problems on linear equations 

Word problems on quadratic equations

Algebra word problems

Word problems on trains

Area and perimeter word problems

Word problems on direct variation and inverse variation 

Word problems on unit price

Word problems on unit rate 

Word problems on comparing rates

Converting customary units word problems 

Converting metric units word problems

Word problems on simple interest

Word problems on compound interest

Word problems on types of angles 

Complementary and supplementary angles word problems

Double facts word problems

Trigonometry word problems

Percentage word problems 

Profit and loss word problems 

Markup and markdown word problems 

Decimal word problems

Word problems on fractions

Word problems on mixed fractrions

One step equation word problems

Linear inequalities word problems

Ratio and proportion word problems

Time and work word problems

Word problems on sets and venn diagrams

Word problems on ages

Pythagorean theorem word problems

Percent of a number word problems

Word problems on constant speed

Word problems on average speed 

Word problems on sum of the angles of a triangle is 180 degree

OTHER TOPICS 

Profit and loss shortcuts

Percentage shortcuts

Times table shortcuts

Time, speed and distance shortcuts

Ratio and proportion shortcuts

Domain and range of rational functions

Domain and range of rational functions with holes

Graphing rational functions

Graphing rational functions with holes

Converting repeating decimals in to fractions

Decimal representation of rational numbers

Finding square root using long division

L.C.M method to solve time and work problems

Translating the word problems in to algebraic expressions

Remainder when 2 power 256 is divided by 17

Remainder when 17 power 23 is divided by 16

Sum of all three digit numbers divisible by 6

Sum of all three digit numbers divisible by 7

Sum of all three digit numbers divisible by 8

Sum of all three digit numbers formed using 1, 3, 4

Sum of all three four digit numbers formed with non zero digits

Sum of all three four digit numbers formed using 0, 1, 2, 3

Sum of all three four digit numbers formed using 1, 2, 5, 6