CONVERTING RADICAL TO EXPONENTIAL FORM

To convert radical to exponential form, let us first consider the equivalent form of radical.

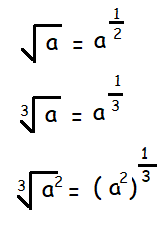
Convert the radical form to exponential form :

Problem 1 :

(⁵√x)³

Solution :

5^th root can be written as power 1/5.

(⁵√x)³ = (x^1/5)³

To simplify the term, which is having a power raised to another power, we can multiply the powers.

(⁵√x)³ = x^{(1/5) x 3}

= x^3/5

Problem 2 :

(³√y⁴)

Solution :

Cube root can be written as power 1/3.

(³√y⁴) = (y⁴)^1/3

= y^4/3

Problem 3 :

(√x⁵)

Solution :

Square root can be written as power 1/2.

(√x⁵) = (x⁵)^1/2

= x^5/2

Problem 4 :

(³√5)³

Solution :

Cube root can be written as power 1/3.

(³√5)³ = (5^(1/3))³

= 5^3/3

= 5

Problem 5 :

√(16x²)

Solution :

Square root can be written as power 1/2.

√(16x²) = (16x²)^1/2

16 can be written as 4²

√(16x²) = (4²x²)^1/2

= ((4x)²)^1/2

= (4x)^{2 ⋅ (1/2)}

= 4x

Problem 6 :

1/(√(6x))³

Solution :

Square root can be written as power 1/2.

1/(√(6x))³ = 1/[(6x)^1/2]³

= 1/(6x)^{(1/2) x 3}

= 1/(6x)^(3/2)

When we move the term from numerator to denominator or denominator to numerator, we have to change the sign of the power.

= (6x)^-3/2

Problem 7 :

1/(⁴√x)⁷

Solution :

Fourth root can be written as power 1/4.

1/(⁴√x)⁷ = 1/(x^1/4)⁷

= 1/x^{(1/4) ⋅ 7}

= 1/x^(7/4)

= x^-7/4

Problem 8 :

1/√(5x)

Solution :

Square root can be written as power 1/2.

1/√(5x) = 1/(5x)^1/2

= (5x)^-1/2

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.