CONVERTING FRACTION TO PERCENTAGE

The process of conversion to percentage from a proper fraction and an improper fraction is same.

There two types of processes in converting a fraction into percentage. 

Type 1 : 

Denominator can be convertible to 100 using multiplication. 

Type 2 : 

Denominator can not be convertible to 100 using multiplication

Type 1 

If denominator of the proper fraction is convertible to 100 using multiplication, we can convert the given proper fraction to percent as explained in the example given below.   

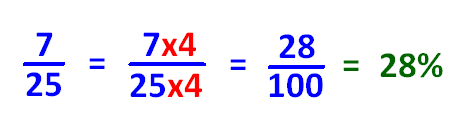
If denominator of the improper fraction is convertible to 100 using multiplication, we can convert the given improper fraction to percent as explained in the example given below.   

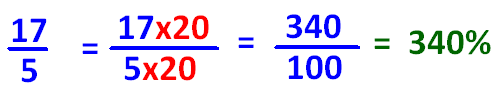
Type 2

If denominator of the proper fraction is not convertible to 100 using multiplication, we have to convert the given proper fraction into decimal. Then we have to convert decimal into percent as explained in the example given below. 

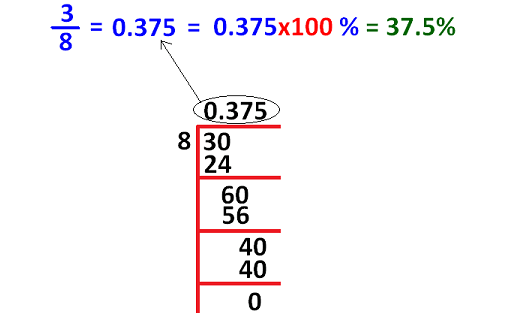
If denominator of the proper fraction is not convertible to 100 using multiplication, we have to convert the given proper fraction into decimal. Then we have to convert decimal into percent as explained in the example given below. 

Practice Problems

Covert the following fractions to percentages.

Problem 1 :

3/4

Solution : 

To convert any fraction to percentage, make the denominator as 100 using multiplication.

In the fraction 3/4, the denominator is 4 which is convertible to 100 using multiplication by 4. 

3/4  =  (3 ⋅ 25) / (4 ⋅ 25)

=  75 / 100

=  75%

Problem 2 :

10/3

Solution :

In the fraction 10/3, the denominator is 3 which can not be converted into 100 or 1000 or 10000 using multiplication. 

So the given fraction can be converted into decimal using long division.  

Then, we have

10/3  ≈  3.3333  (approximately)

Multiply 3.3333 by 100 to convert it to percentage.

3.3333 ⋅ 100%  ≈  333.33%

Problem 3 :

5/8

Solution : 

To convert any fraction to percentage, make the denominator as 100 using multiplication.

In the fraction 5/8, the denominator is 8 which which can not be converted into 100 using multiplication. 

But 8 can be converted into 1000 using multiplication of 125.

Then, 

5/8  =  (5 ⋅ 125) / (8 ⋅ 125)

=  625/1000

=  0.625

Multiply 0.625 by 100 to convert it to percentage.

0.625 ⋅ 100%  =  62.5%

Problem 4 :

3 1/8

Solution : 

To convert the given mixed number to percentage, first convert the given mixed number into improper fraction.

3 1/8  =  25/8

To convert any fraction to percentage, we have to make the denominator as 100 using multiplication.

In the fraction 25/8, the denominator is 8 which can not be converted into 100 using multiplication. 

But 8 can be converted to 1000 using multiplication of 125.

Then, 

25/8  =  (25 ⋅ 125) / (8 ⋅ 125)

=  3125 / 1000

=  3.125

Multiply 3.125 by 100 to convert it to percentage.

3.125 ⋅ 100%  =  312.5%

Problem 5 :

A rectangular pizza is cut into 20 pieces as shown. Chilli has been put on 4 pieces.

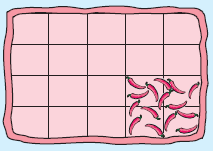
a) What fraction of the pizza does not have chilli?

b) What percentage of the pizza does not have chilli?

c) What percentage of the pizza does have chilli?

Solution :

a)  Total number of squares = 20

Number of squares in which we have chillis = 4

Number of square that we doesn't have chillis = 20 - 4

= 16

The fractions of pizza does not have chilli = 16/20

After the simplification, we get 4/5

b)  To convert this fraction as percentage, we have to multiply the above fraction by 100%

= (4/5) x 100%

= 4 x 20%

= 80%

c) Percentage of pizza does have chilli

The total quantity can be considered as 100%,

= (100 - 80)%

= 20%

Problem 6 :

A bus has 25 seats. 10 seats are occupied by passengers.

a) What fraction of the seats are occupied?

b) What percentage of the seats are occupied?

c) What percentage of the seats are unoccupied?

Solution :

Total number of seats = 25

Number of seats occupied = 10

Number of seats free = 25 - 10

= 15

a) Fraction of the seats are occupied = 10/25

= 2/5

b) Percentage of the seats are occupied

To convert into percentage, we have to multiply by 100%.

= (2/5) x 100%

= 2 x 20%

= 40%

c) Percentage of the seats are unoccupied

= (100 - 40)%

= 60%

A window consists of 16 panes of glass as shown.

The outer 12 panes are coloured blue.

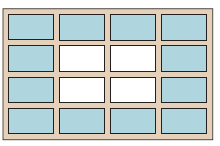
a) What fraction of the window is blue?

b) What percentage of the window is blue?

c) What percentage of the window is not blue?

Solution :

a)  Fraction part of window which are blue = 12

Fraction of window which is blue = 12/16

Doing the simplification, we get

= 3/4

b) Percentage of window which is blue :

= (3/4) x 100%

= 3 x 25%

= 75%

c) Percentage of window which is not blue 

= (100 - 75)%

= 25%

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.