CONVERT THE GIVEN COMPLEX NUMBER FROM RECTANGULAR TO POLAR FORM

To represent complex numbers x + iy geometrically, we use the rectangular coordinate system with the horizontal axis representing the real part and the vertical axis representing the imaginary part of the complex number. 

This representation is known as rectangular form or argand plane  of a complex number.

r(cosθ + isinθ) is known as polar form.

Here r stands for modulus and θ stands for argument

To find the modulus value of given complex number in the form of a + ib, we have to use the formula √(a² + b²). 

Usually we have two methods to find the argument of the given complex number.

How to find argument of complex number

Usually we have two methods to find the argument of a complex number

(i) Using the formula θ = tan^-1(y/x).   

Here x and y are real and imaginary part of the complex number respectively.

This formula is applicable only if x and y are positive.

(ii) But the following method is used to find the argument of any complex number.  

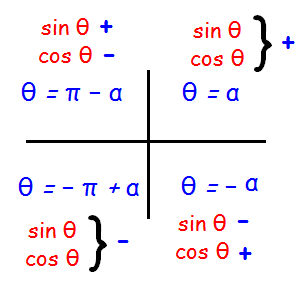
Example 1 :

Convert the given complex number from rectangular to polar form

- √2 + i√2

Solution :

- √2 + i√2  =  r(cosθ  + i sinθ) ----(1)

r = √[(-√2)² + (√2)²] = √(2 + 2) = √4 = 2

r = 2

Apply the value of r in the first equation

- √2 + i√2  =  2(cosθ  + isinθ)

- √2 + i√2  =  2cosθ + i2sinθ

Equating the real and imaginary parts separately

Since sinθ is positive and cosθ is negative the required angle θ lies in the second quadrant.

θ  =  Π - α

Here α is nothing but the angles of sin and cos for which we get the value 1/√2

θ  =  Π - (Π/4)

θ  =  (4Π-Π)/4  =  3Π/4

Modulus = 2 and argument = 3Π/4

Hence, the polar form of the given complex number :

2(cos 3Π/4  + i sin 3Π/4)

Example 2 :

Convert the given complex number from rectangular to polar form

1 + i√3

Solution :

1 + i√3 = r(cosθ + isinθ) ----(1)

r = √[(1)² + (√3)²] = √(1 + 3) = √4 = 2

r = 2

Apply the value of r in the first equation

1 + i√3  =  2(cosθ + isinθ)

1 + i√3  =  2cosθ + i2sinθ

Equating the real and imaginary parts separately

Since sinθ and cosθ are positive, the required angle θ lies in the first quadrant.

θ  =  α

Here α is nothing but the angles of sin and cos for which we get the values 1/2 and √3/2 respectively.

θ  =  Π/3

Modulus = 2 and argument = Π/3

Hence, the polar form of the given complex number :

2(cos Π/3 + i sin Π/3)

Example 3 :

Convert the given complex number from rectangular to polar form

-1 - i√3

Solution :

-1 - i√3  =  r(cosθ + isinθ) ----(1)

r  =  √[(-1)² + (-√3)²]  =  √(1 + 3)  =  √4  =  2

r  =  2

Apply the value of r in the first equation

-1 - i√3  =  2(cosθ + isinθ)

-1 - i√3  =  2cosθ + i2sinθ

Equating the real and imaginary parts separately

Since sin θ and cos θ are negative the required angle θ lies in the third quadrant.

θ  =  -Π + α

Here α is nothing but the angles of sin and cos for which we get the values √3/2 and 1/2 respectively.

θ  =  -Π + α

     =  -Π + Π/3  =  (-3Π+Π)/3  =  -2Π/3

Modulus = 2 and argument =-2Π/3

Hence, the polar form of the given complex number :

2(cos (-2Π/3)  + i sin (-2Π/3))

Example 4 :

Convert the given complex number from rectangular to polar form

√21 + i√7

Solution :

√21 + i√7 =  r(cosθ + isinθ) ----(1)

r  =  √[(√21)² + (√7)²]  =  √[21 + 7]  = √28

r = 2√7

Apply the value of r in the first equation

√21 + i√7= 2√7(cosθ + isinθ)

Equating the real and imaginary parts separately

Since sin θ and cos θ are negative the required angle θ lies in the first quadrant.

θ = α

Here α is nothing but the angles of sin and cos for which we get the values 1/2 and √3/2 respectively.

θ = α

     = Π/3

Modulus = 2√7 and argument = Π/3

Hence, the polar form of the given complex number :

2√7[cos(Π/3)  + i sin (Π/3)]

Example 5 :

Convert the given complex number from rectangular to polar form

-5√2/2 - i(5√2/2)

Solution :

-5√2/2 - i(5√2/2) = r(cosθ + isinθ) ----(1)

r  =  √[-5√2/2)² + (-5√2/2)²]  =  √(50 + 50)/4  = √25

r = 5

Apply the value of r in the first equation

-5√2/2 - i(5√2/2) = 5(cosθ + isinθ)

Equating the real and imaginary parts separately

Since sinθ is negative and cos θ is negative, the angle lies in the third quadrant.

θ  =  -Π + α

Here α is nothing but the angles of sin and cos for which we get the values √2/2 and √2/2 respectively.

θ = -Π + (Π/4)

= (-4Π + Π)/4

= -3Π/4

Modulus = 5 and argument = -3Π/4

Hence, the polar form of the given complex number :

2√7[cos (-3Π/4)  + i sin (-3Π/4)]

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.