CONVERT EQUATIONS OF PARABOLAS FROM GENERAL TO VERTEX FORM

Vertex form equation of a parabola : 

(y - k) = ± a(x - h)²

(i)  If "a" is positive, the parabola opens upward. If it is negative, then the parabola opens downward.

(ii)  First we have to check whether the coefficient of x² is 1 or not. If yes we can follow the second step. Otherwise factor out the coefficient of x² from the equation.

(iii) Keep the x² and x terms in the right side and keep the y-term and constant term to the left side.

(iv)  Add the square of half of the coefficient of "x" on both sides.

(v) Now the three terms on the right side will be in the form of a² + 2ab + b² (or) a² - 2ab + b².

a² + 2ab + b²  =  (a + b)²

a² - 2ab + b²  =  (a - b)²

(vi)  Now we can get the vertex from this equation.

Vertex of the parabola V (h, k)

Example 1 :

Use the information provided to write the vertex form equation of each parabola and sketch the parabola.

y  =  x² - 4x + 3

Solution :

Step 1 :

The coefficient of x² is 1.

Step 2 :

Subtract 3 on both sides.

y - 3  =  x² - 4x + 3 - 3

y - 3  =  x² - 4x

Step 3 :

Half of the of coefficient of x is 2.

Square of half of the coefficient of x is 2²  =  4.

y - 3 + 4  =  x² - 4x + 4

y - 3 + 4  =  x² - 2⋅x⋅2 + 2²

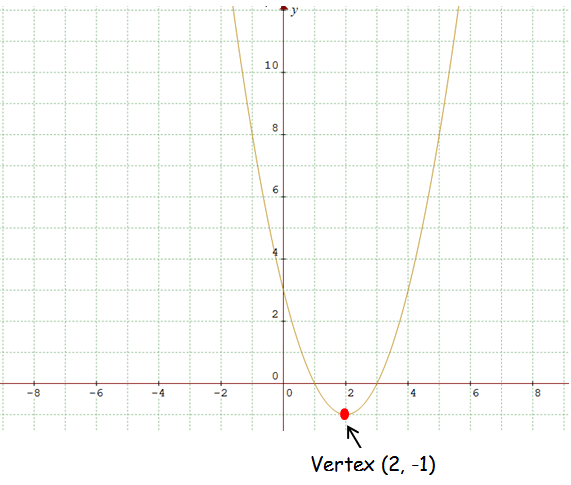
y + 1  =  (x - 2)²

Step 4 :

By comparing the above equation with vertex form

(y - k)  =  a(x - h)²

we can get the vertex. 

(h, k)  ==>  (2, -1)

Since the coefficient of x² is positive the parabola opens upward.

Example 2 :

Use the information provided to write the vertex form equation of each parabola and sketch the parabola.

y  =  2x² - 8x + 9 

Solution :

Step 1 :

The coefficient of x² is not 1, we have to divide the equation on the right side by 2.

y - 9  =  2x² - 8x 

y - 9  =  2(x² - 4x)

Step 2 :

y - 9  =  2(x² - 2 x 2 + 2² - 2²)

y - 9  =  2[(x - 2)² - 4]

y - 9  =  2(x - 2)² - 8

y - 9 + 8  =  2(x - 2)² - 8 + 8

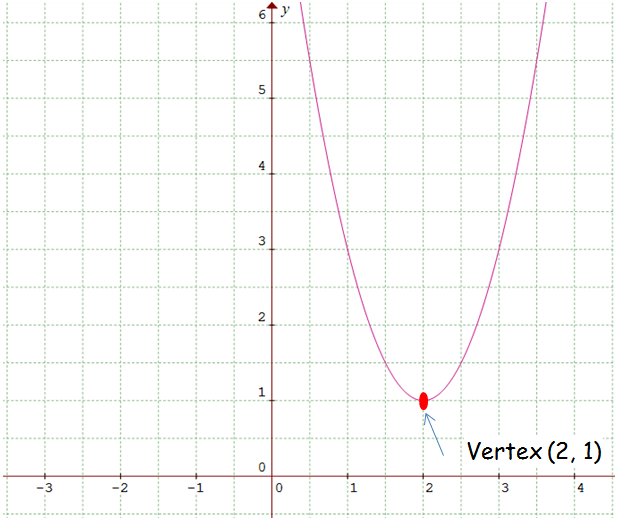
y - 1  =  2 (x - 2)²

Vertex of the parabola is (2, 1).

Example 3 :

Use the information provided to write the vertex form equation of each parabola and sketch the parabola.

y  =  x² - 6x + 5

Solution :

Step 1 :

The coefficient of x² is 1.

Step 2 :

Subtract 5 on both sides.

y - 5  =  x² - 6x + 5 - 5

y - 5  =  x² - 6x

Step 3 :

Half of the of coefficient of x is 3.

Square of half of the coefficient of x is 3²  =  9.

y - 5 + 9  =  x² - 6x + 9

y + 4  =  x² - 2⋅x⋅3 + 3²

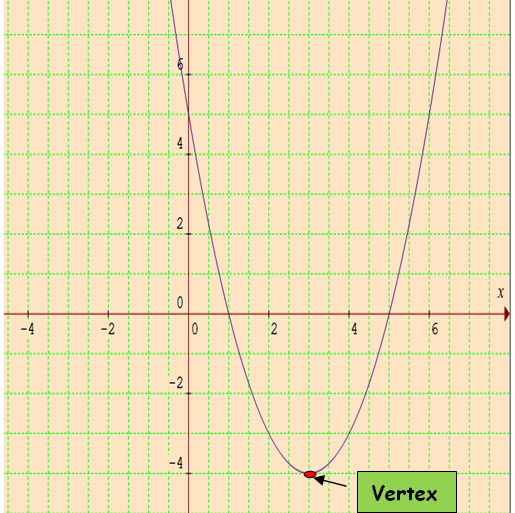
y + 4  =  (x - 3)²

Step 4 :

By comparing the above equation with vertex form

(y - k)  =  a(x - h)²

we can get the vertex. 

(h, k)  ==>  (3, -4)

Since the coefficient of x² is positive the parabola opens upward.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.