CONVERT BETWEEN PERCENTS FRACTIONS AND DECIMALS WORKSHEET

Problems 1-4 : Convert the percentage to proper fraction.

Problem 1 :

2.4%

Problem 2 :

0.55%

Problem 3 :

0.25%

Problem 4 :

15%

Problem 5 :

Convert the percentage to an improper fraction.

125%

Problems 6-10 : Covert the fraction to decimal.

Problem 6 :

3/20

Problem 7 :

7/10

Problem 8 :

3/50

Problem 9 :

 1/2

Problem 10 :

 3/4

Problems 11-15 : Convert the fraction to percentage.

Problem 11 : 

2/3

Problem 12 : 

5/6

Problem 13 : 

5/12

Problem 14 : 

45/8

Problem 15 : 

10/3

Problem 16 : 

In an election, the winning candidate receives 60% of the votes. What percent of the votes does the other candidate receive?

Problem 17 : 

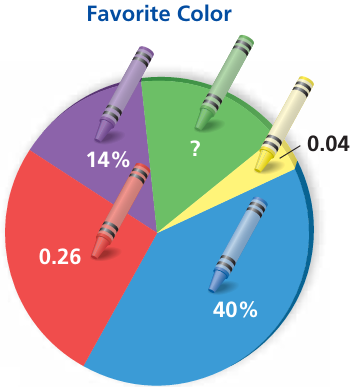
Students in a class were asked to tell their favorite color.

a. What percent said red, blue, or yellow?

b. How many times more students said red than yellow?

c. Use two methods to find the percent of students who said green. Which method do you prefer?

Problem 18 : 

In the first 42 Super Bowls, 0.16 of the MVPs (most valuable players) were running backs.

a. What percent of the MVPs were running backs?

b. What fraction of the MVPs were not running backs?

Problem 19 : 

How would you decide whether 3/5 or 59% is greater? Explain.

Problem 20 : 

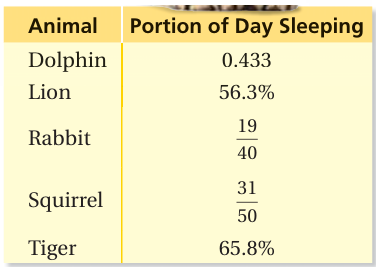
The table shows the portions of the day that several animals sleep.

a. Order the animals by sleep time from least to greatest.

b. Estimate the portion of the day that you sleep.

c. Where do you fit on the ordered list?

1. Answer :

2.4% = 2.4/100

= 24/1000

= 3/125

2. Answer :

0.55% = 0.55/100

= 55/10000

= 11/2000

3. Answer :

0.25% = 0.25/100

= 25/10000

= 1/400

4. Answer :

15% = 15/100

= 3/20

5. Answer :

125% = 125/100

= 5/4

6. Answer :

In the given fraction 3/20, the denominator 20 is convertible to 100.

So, we have 

3/20 = (3 ⋅ 5)/(20 ⋅ 5)

= 15/100

= 0.15

7. Answer :

In  the fraction 7/10, the denominator is 10. 

So, we have 

7/10 = 0.7

8. Answer :

In the fraction 3/50, the denominator 50 is convertible to 100. 

3/50 = (3 ⋅ 2)/(50 ⋅ 2)

= 6/100

= 0.06

9. Answer :

In the fraction 1/2, the denominator 2 is convertible to 10. 

1/2 = (1 ⋅ 5)/(2 ⋅ 5)

= 5/10

= 0.5

10. Answer :

In  the fraction 3/4, the denominator 4 is convertible to 100. 

So, we have 

3/4 = (3 ⋅ 25)/(4 ⋅ 25)

= 75/100

= 0.75

11. Answer :

In the fraction 2/3, the denominator 3 can't be converted to 10 or 100. 

So, 2/3 can be converted to decimal using long division. 

Then, we have

2/3 ≈ 0.6667

0.6667 = 0.6667 ⋅ 100%

= 66.67%

Therefore, 

2/3 ≈ 66.67%

12. Answer :

In the fraction 5/6, the denominator 6 can't be converted to 10 or 100. 

So, 5/6 can be converted to decimal using long division.  

Then, we have

5/6 ≈ 0.8333

0.8333 = 0.8333 ⋅ 100%

= 83.33%

Therefore, 

5/6 ≈ 83.33%

13. Answer :

In the fraction 5/12, the denominator 12 can't be converted to 10 or 100. 

So, 5/12 can be converted to decimal using long division.

Then, we have

5/12 ≈ 0.4167

0.4167 = 0.4167 ⋅ 100%

= 41.67%

Therefore, 

5/12 ≈ 41.66%

14. Answer :

In the fraction 45/8, the denominator 8 can't be converted to 10 or 100. 

So, 45/8 can be converted to decimal using long division.

45/8 = 5.625

= 5.625 ⋅ 100%

= 562.5%

15. Answer :

In the fraction 10/3, the denominator 3 can't be converted to 10 or 100.

So, 10/3 can be converted to decimal using long division.  

Then, we have

10/3 ≈ 3.3333

3.3333 = 3.3333 ⋅ 100%

= 333.33%

Therefore,

10/3 ≈ 333.33%

16. Answer :

Percentage of votes recieved by winning candidate = 60%

Percentage of the votes the other candidate receive

= 100% - 60%

= 40%

17. Answer :

a.

Percentage of students who said red = 0.26

= 0.26 x 100%

= 26%

Percentage of students who said blue = 40%

Percentage of students who said yellow = 0.04

= 0.04 x 100%

= 4%

b. Required number of times = 26/4

= 13/2

= 6.5 times

c. Percentage of students who said green

Method 1 :

= 100% - (14 + 26 + 40 + 4)%

= 100% - 84%

= 16%

Method 2 :

= 0.26 + 0.40 + 0.04 + 0 .14

= 0.84

Converting into percentage, we get

= 0.84 x 100%

= 84%

I prefer method 1.

18. Answer :

Number of super bowls = 42

Number of MVPs were running back = 0.16

a) Percentage of MVPs running back = 0.16/42

= 0.0038.....

To convert into percentage, we have to multiply by 100%, we get

= 0.0038....... x 100%

= 0.38%

b) Percentage of MVP's not running backs

= (100 - 0.38)%

= 99.62%

19. Answer :

To compare two numbers which are in different forms, we have make it into same form and then do the comparision.

= 3/5

= (3/5) x 100%

= (3 x 20)%

= 60%

Comparing 60% and 59%, 60 % is greater. Then 3/5 is greater.

a. To arrange into least to greatest, we have convert all number forms in the same representation.

Let us convert everything into percentage,

Dolphin :

= 0.433

= 0.433 x 100%

= 43.3%

Lion :

= 56.3%

Rabbit :

= 19/40

= (19/40) x 100%

= 0.475 x 100%

= 47.5%

Squirrel :

= 31/50 x 100%

= 31 x 2%

= 62%

Tiger :

= 65.8%

Ordering from least to greatest,

43.3%, 47.5%, 56.3%, 62%, 65.8%

b.

• Dolphin is spending 43.3% on sleep.
• Rabbit is spending 47.5% of on sleep
• Lion is spending 56.3% of on sleep
• Squirrel is spending 62% of on sleep
• Tiger  is spending 65.8% of on sleep

c. Dolphin, abbit, Lion, Squirrel, Tiger

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.