CONSTRUCTION OF PARALLEL LINES

Parallel lines are the lines which will never intersect and the perpendicular distance between them will be same at everywhere.

Let us see how to construct parallel lines.

Steps to Construct Parallel Lines

Using a set square and a ruler draw a line parallel to a given line through a point at a distance of 5cm above it.

Step 1 :

(i) Draw a line XY using ruler and mark a point A on it.

(ii) Draw AM = 5cm with the help of a set square.

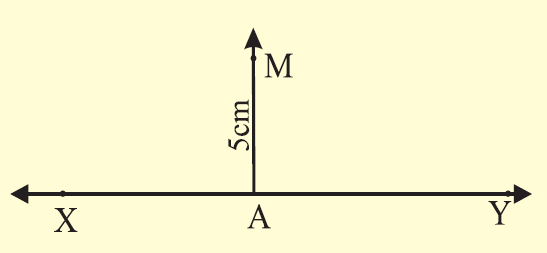
Step 2 :

Place the set square on the line segment XY.

(i) Place the set scale as shown in the figure.

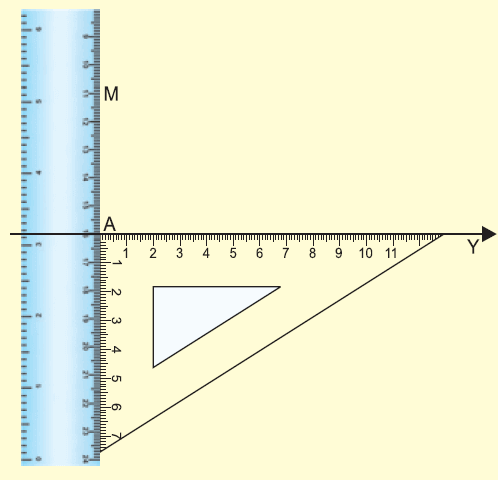
Step 3 :

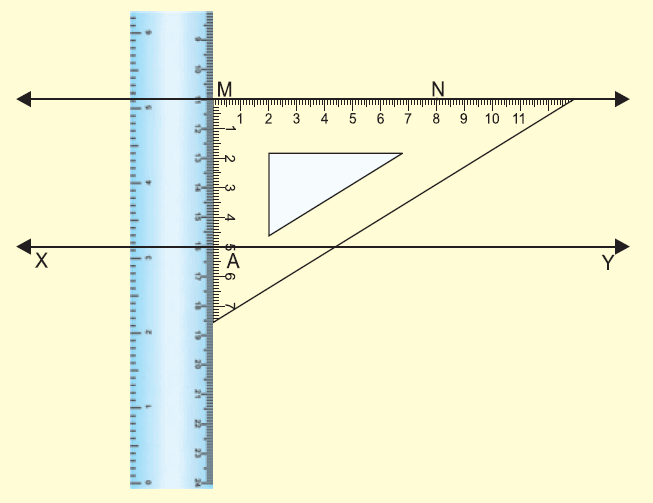
(i) Pressing tightly the ruler, slide the set square along the ruler till the edge of the set square touches the point M.

(ii) Through M, draw a line MN along the edge.

(iii) MN is the required line parallel to XY through M.

Properties of Parallel Lines

When we construct parallel lines, we have to confirm that the parallel lines constructed by us must meet the following properties. 

(i)  Let m₁ and m₂ be the slopes of two lines.

If, the two lines are parallel, then their slopes will be equal.

That is, 

m₁  =  m₂

(ii) Let us consider the general form of equation of a straight line ax + by + c  =  0.  

If the two lines are parallel, then their general form of equations will differ only in the constant term and they will have the same coefficients of "x" and "y". 

That is, 

ax + by + c₁  =  0

ax + by + c₂  =  0

(iii)  Let us consider the slope intercept form of equation of a straight line  y  =  mx + b.  

If the two lines are parallel, then their slope-intercept form equations will will differ only in the "y"- intercept. 

That is, 

y = mx + b₁

 y = mx + b₂

(iv)  Let l₁ and l₂ be two lines.

If the two lines are parallel, the angle between them and the positive side of x-axis will be equal. 

The figure given below illustrates the above situation.

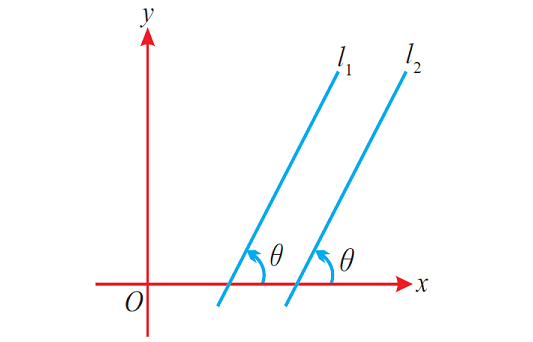
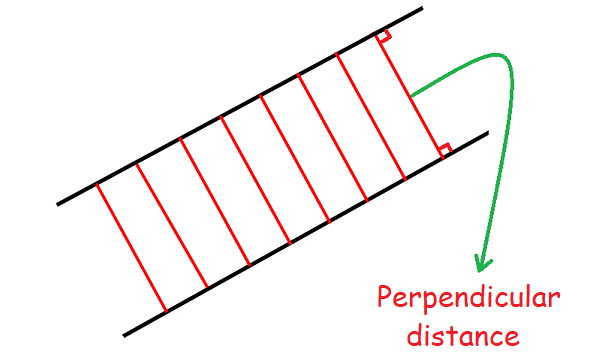
(v) If the two lines are parallel, the perpendicular distance between them will be same at everywhere. 

The figure given below illustrates the above situation.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.