CONSTRUCTION OF ORTHOCENTER OF A TRIANGLE

In this section, you will learn how to construct orthocenter of a triangle. 

Key Concept - Orthocenter

The point of concurrency of the altitudes of a triangle is called the orthocenter of the triangle and is usually denoted by H.

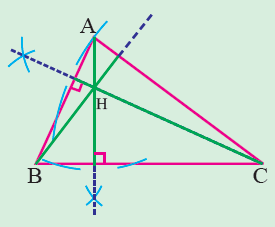
Before we learn how to construct orthocenter of a triangle, first we have to know how to construct altitudes of triangle. 

So, let us learn how to construct altitudes of a triangle. 

Constructing Altitudes of a Triangle

To construct a altitude of a triangle, we must need the following instruments.

1. Ruler

2. Compass

The steps for the construction of altitude of a triangle.

Step 1 :

Draw the triangle ABC as given in the figure given below.

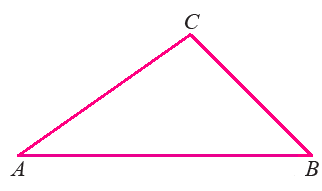
Step 2 :

With C as center and any convenient radius draw arcs to cut the side AB at two points P and Q.

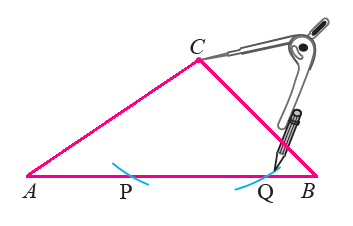
Step 3 :

With P and Q as centers and more than half the distance between these points as radius draw two arcs to intersect each other at E.

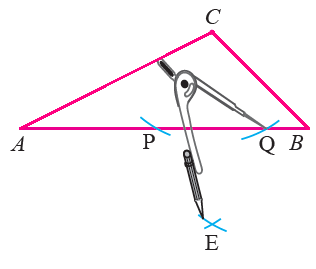
Step 4 :

Join C and E to get the altitude of the triangle ABC through the vertex A. 

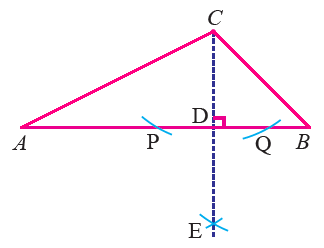
In the above figure, CD is the altitude of the triangle ABC. 

This construction clearly shows how to draw altitude of a triangle using compass and ruler. 

As we have drawn altitude of the triangle ABC through vertex A, we can draw two more altitudes of the same triangle ABC through the other two vertices.  

Therefore, three altitude can be drawn in a triangle. 

Now, let us see how to construct the orthocenter of a triangle. 

Constructing Orthocenter of a Triangle - Steps

To construct orthocenter of a triangle, we must need the following instruments.

1. Ruler

2. Compass

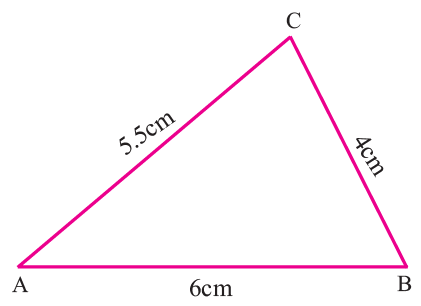
Construct triangle ABC whose sides are AB = 6 cm, BC = 4 cm and AC = 5.5 cm and locate its orthocenter.

Step 1 :

Draw the triangle ABC with the given measurements.     

Step 2 :

Construct altitudes from any two vertices (A and C) to their opposite sides (BC and AB respectively).

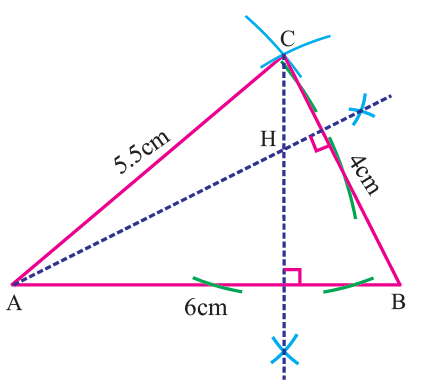
The point of intersection of the altitudes H is the orthocenter of the given triangle ABC.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.