CONSTRUCTION OF LINE SEGMENT

A line segment is the shortest that connects two given points, but a line has no end points.

The line segment joining the two points A and B can be simple written as AB or the line segment AB. 

Length of the line segment AB is equal to the length of the line segment BA.

A line segment can be measured either with a ruler or divider.

Let us look at some examples to understand how to construct a line segment. 

Example 1 :

Draw a line segment AB  =  5.8 cm using a ruler. 

Step 1 : 

Draw a line "l" and mark a point A on it. 

Step 2 : 

Fix a ruler on the line. Fix it in such a way that the zero on the scale and the point "A" coincides. 

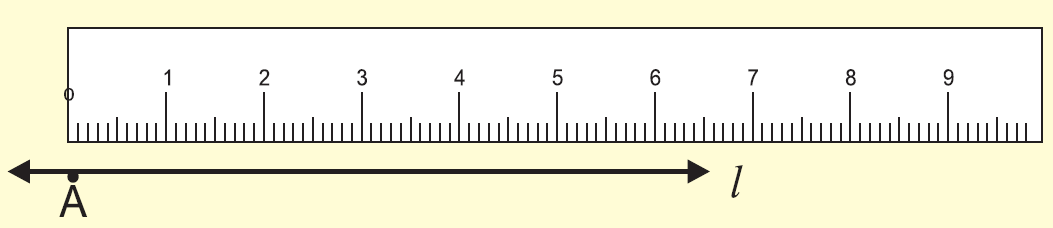
Step 3 : 

(i) From A, measure 5.8 cm

(ii) Mark the point as B.

(iii) AB = 5.8 cm is the required segment. 

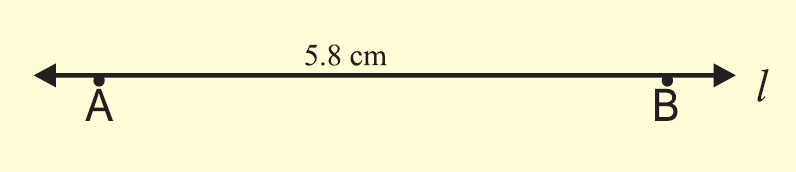
Example 2 :

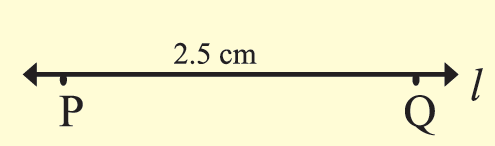
With the help of a ruler and compass, draw a line segment PQ  =  2.5 cm 

Step 1 : 

Draw a line "l" and mark a point P on it. 

Step 2 : 

With the help of a compass, measure 2.5 cm as shown in the figure. 

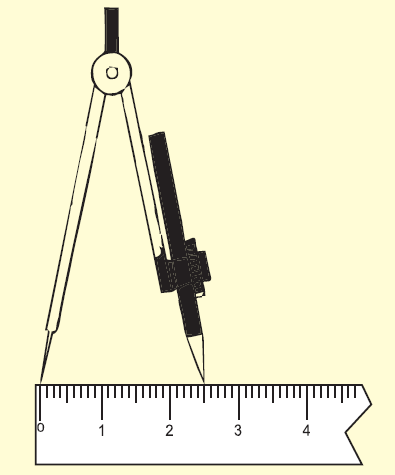
Step 3 : 

(i) Place the sharp edge of the compass at P. 

(ii) Then with the pencil, draw a small arc on "l" to cut the line. mark the point as "Q". 

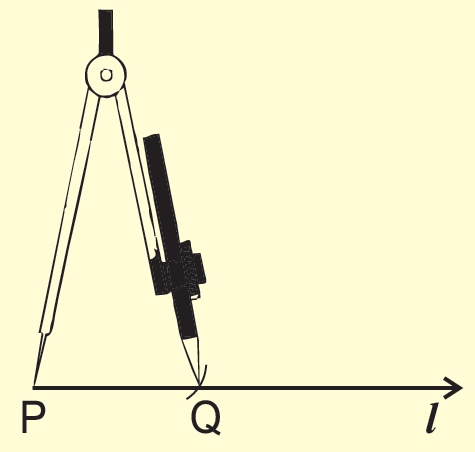
(iii) PQ = 2.5 cm is the required line segment. 

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.